قوانین احتمال

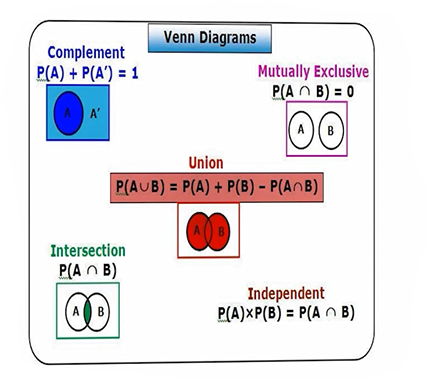
احتمال در نمودار Venn

• توسعه روابط احتمالی بر اساس نظریه مجموعه ها؛
• فضای احتمال در مستطیل نمایش داده می شود.
• پیش آمد احتمال با A نشان داده میشود.

سوال: چرا در نمودار Venn روبرو که معقوله اجتماع مطرح شده است باید سهم اشتراک احتمال های A و B باید کسر شود؟

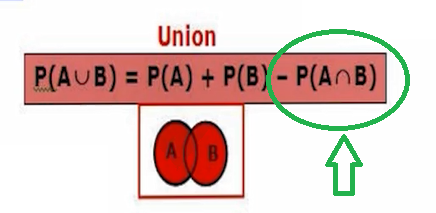
پاسخ: چون احتمال اشتراک در هر دو احتمال های P(A) و P(B) دیده شده است و برای اینکه یکی از دوبار حذف شود یکبار باید عبارت منهای احتمال اشتراک شود.

پیشامد های ناسازگار و قانون جمع احتمال

به پیشامد هایی که امکان وقوع همزمان آن ها ممکن نیست؛ مثلاً پیش آمد حرکت به سمت جلو و عقب به صورت همزمان، پیشامد سمت شیر و خط سکه به صورت همزمان و…

پیشامدهای مستقل و قانون ضرب احتمال

دو پیشامدی که وقوع یا عدم وقوع یکی از آنها، تاثیری در وقوع یا عدم وقوع دیگری ندارد، مثلاً احتمال مرد بودن و داشتن گروه خونی O، بارندگی هوا و برنده شدن در لاتاری و …

نکته: در حالت فوق احتمال توام دو پیشامد، برابر حاصل ضرب احتمالات آن هاست.

پیشامد وابسته: پیشامدهایی که احتمال وقوع آنها می تواند بر روی هم تاثیر بگذارد. مثلا حضور ما در یک مهمانی به حضور یا عدم حضور فرد دیگری وابسته باشد.

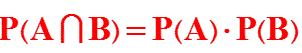
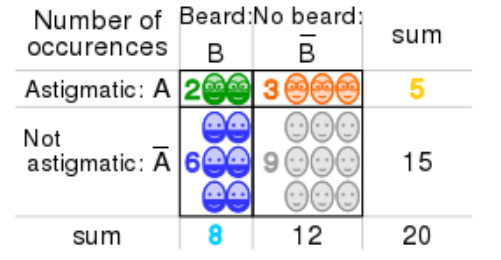
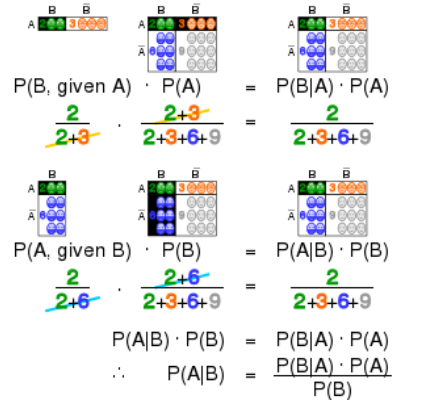
احتمال شرطی:

در بسیاری از پدیده های تصادفی، اغلب آگهی از رخداد پیشامد B در محاسبه احتمال پیشامد A تاثیر می گذارد.

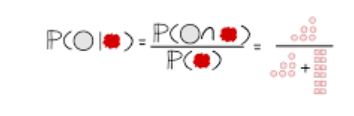
احتمال A  به شرط B یا (A|B)P به این معنا است که احتمال وقوع A را میخواهیم بدانیم در شرایطی که B اتفاق افتاده باشد و این بدین معناست که فضای نمونه به B کاهش پیدا کرده است.

سوال: احتمال دایره بودن در شکل زیر به شرط آنکه رنگ آن قرمز باشد چقدر است؟

پاسخ:

سوال: در جدول زیر احتمال اینکه دانشجو چهار بار یا بیشتر در آموزش شرکت کرده باشد به شرط آنکه فول تایم باشد را محاسبه کنید؟

پاسخ:

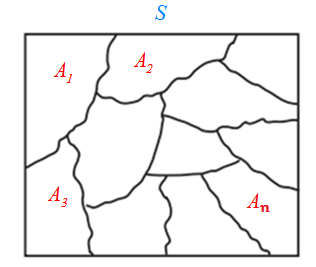
قانون افراز

فرض کنیم A₁,A₂,A₃,….A_n  زیرمجموعه‌های ناتهی از مجموعه فضای نمونه  S باشند، در این‌صورت می‌گوییم این مجموعه‌ها یک افراز روی S درست کرده‌اند به‌شرط آن‌که داشته باشیم:

مثلاً به‌عنوان نمونه: کشور ایران به 31 استان افراز شده است.

 قانون احتمال کل

اگر S  فضای نمونه آزمایش تصادفی باشد و پیشامدهای ناسازگار  A₁,A₂,A₃,….A_n یک افراز روی  S تشکیل داده باشند، آن‌گاه برای هر پیشامد  B در S داریم:

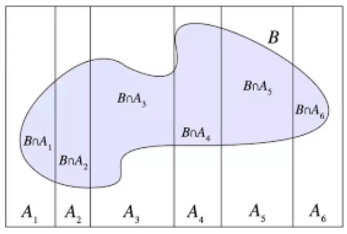
P(B)=P(B ∩A1 )+ P(B ∩A2 )+ P(B ∩A3 )+ P(B ∩A4 )+ P(B ∩A5 ) + P(B ∩A6 )  =

P(B|A1) P(A1) + P(B|A2) P(A2)+ P(B|A3) P(A3)+ P(B|A4) P(A4)+ P(B|A5) P(A5)+ P(B|A6) P(A6) =

قضیه بیز (Bayes Theorem)

روشی برای دسته بندی پدیده ها بر اساس احتمال وقوع یا عدم وقوع یک پدیده.

این قضیه از آن جهت مفید است که می‌توان از طریق آن، احتمال یک پیشامد را با مشروط کردن نسبت به وقوع یا عدم وقوع یک پیشامد دیگر محاسبه کرد. در بسیاری از حالت‌ها، محاسبه احتمال یک پیشامد به صورت مستقیم کاری دشوار است. با استفاده از این قضیه و مشروط کردن پیشامد مورد نظر نسبت به پیشامد دیگر، می‌توان احتمال مورد نظر را محاسبه کرد.