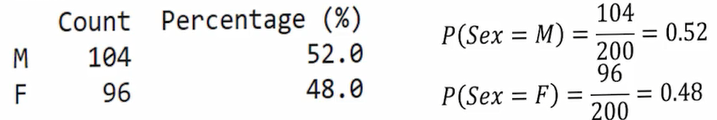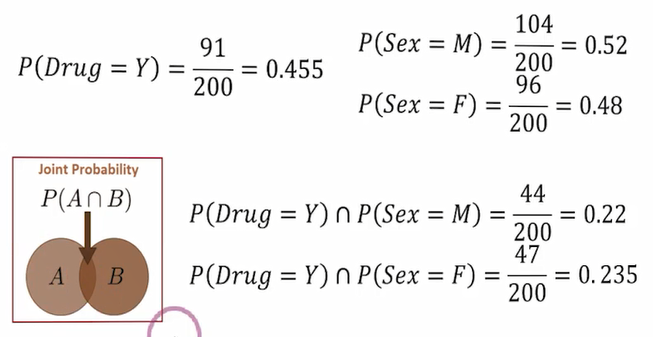در این جلسه به مباحث پایهای و بنیادی تئوری احتمال میپردازیم. پیشتر دربارهی تفاوت میان آمار و احتمال صحبت شد و اکنون قصد داریم بهصورت عمیقتر وارد مفاهیم تئوری احتمال شویم. این بخش در واقع همان بخش انتزاعی و نظری است که زیرساخت تمام ابزارهای آماری و مدلهای مورد استفاده در علم داده محسوب میشود.
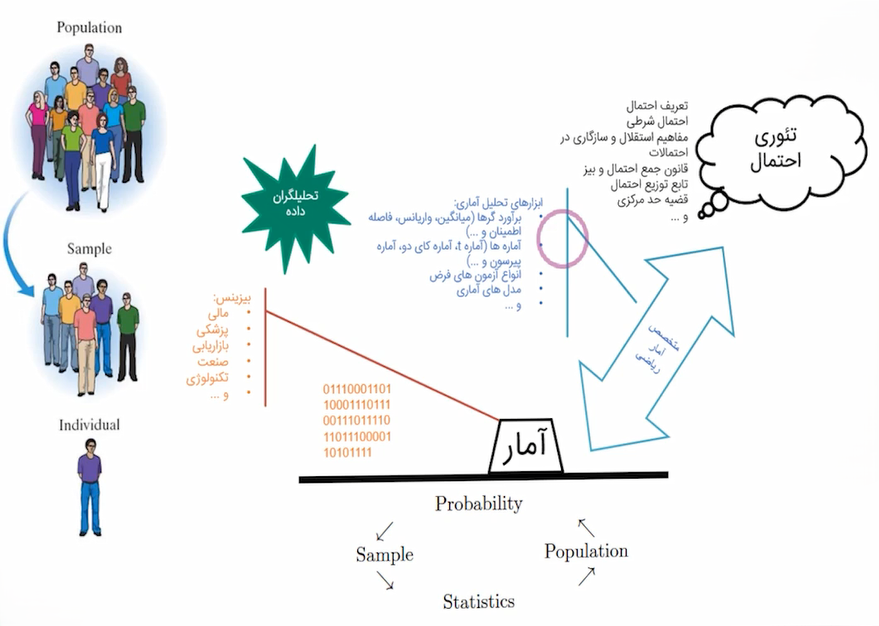
تفاوت آمار و احتمال
-
تئوری احتمال: فضایی انتزاعی و ریاضیاتی دارد. در آن، مدلها و اثباتهای ریاضی مطرح میشوند که مبنای نظری ابزارهای آماری هستند.
-
آمار: دادهها را از دنیای واقعی (صنعت، کسبوکار و …) جمعآوری کرده و با استفاده از ابزارهای ساختهشده بر مبنای تئوری احتمال، تجزیهوتحلیل انجام میدهد.
به بیان دیگر:
-
احتمال از کل به جزء حرکت میکند؛ یعنی از جامعه (Population) به نمونه (Sample).
-
آمار از جزء به کل حرکت میکند؛ یعنی از نمونه به جامعه تعمیم میدهد.
جامعه و نمونه
در دنیای واقعی معمولاً به کل جامعه دسترسی نداریم؛ زیرا جامعه بزرگ است و بررسی تمام اعضا بسیار زمانبر، پرهزینه و در بسیاری موارد غیرممکن است. برای مثال، سرشماری جمعیت یک کشور هر ماه یا هر سال انجام نمیشود؛ بلکه معمولاً هر ۵ یا ۱۰ سال یکبار اجرا میگردد، چرا که پروژهای ملی، زمانبر و پرهزینه است.
بنابراین در تحلیل دادهها اغلب با نمونه (Sample) سروکار داریم. نمونه زیرمجموعهای از جامعه است که از آن برای تخمین ویژگیهای جامعه استفاده میکنیم. پارامترهای جامعه غالباً ناشناختهاند و آمار با تحلیل نمونهها تلاش میکند این پارامترها را تخمین بزند.
تعریف احتمال
احتمال به زبان ساده، نسبت فراوانی وقوع یک رویداد به کل فضای نمونه است.
مثال ساده: تاس
اگر یک تاس سالم پرتاب کنیم:
-
فضای نمونه شامل شش حالت (۱ تا ۶) است.
-
احتمال آمدن عدد ۱ برابر با 1/6 است.
-
این تعریف زمانی صادق است که تاس منصفانه باشد (بایاس یا انحراف نداشته باشد).
مثال کاربردی: دادههای دارو
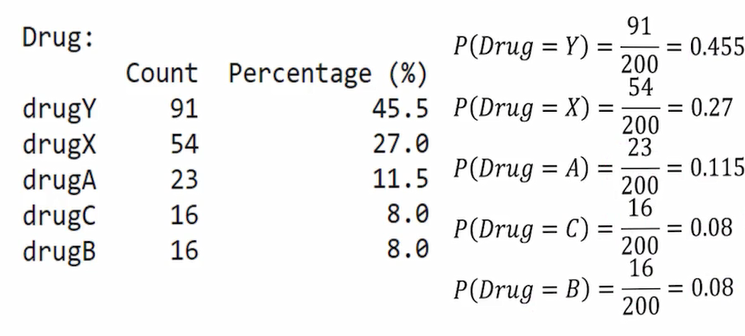
در دادههای مربوط به بیماران کلینیک، برای داروی Y مشاهده کردیم که از مجموع ۲۰۰ بیمار، ۹۱ نفر آن را دریافت کردهاند.
-
احتمال تجویز داروی Y برابر با ۴۵٪ است.
-
احتمال تجویز داروی X برابر با ۲۷٪ بود (۵۴ نفر از ۲۰۰ نفر).
-
داروی A حدود ۱۱–۱۲٪، داروی C حدود ۸٪ و داروی B نیز حدود ۸٪ احتمال داشتند.
اگر بیماری وارد کلینیک شود و هیچ اطلاعی از شرایطش نداشته باشیم، محتملترین پیشبینی این است که داروی Y برای او تجویز شود، زیرا بیشترین احتمال (۴۵٪) را دارد.
ارتباط با مدلسازی
این همان کاری است که مدلهای آماری و یادگیری ماشین در نهایت انجام میدهند: محاسبهی احتمال وقوع رویدادها.
-
در یک مسئلهی دستهبندی (Classification)، اگر احتمال وقوع هر کلاس محاسبه شود، کلاس با بیشترین احتمال به عنوان پیشبینی انتخاب میشود.
-
در مثال ما، بدون استفاده از هیچ متغیر کمکی، تنها با مشاهدهی توزیع دادهها توانستیم مدلی بسازیم که دقت آن حدود ۴۵٪ است.
این در حقیقت اولین نمونهی ساده از یک مدل دادهکاوی است.
احتمال و ویژگیهای دیگر داده
مثال: جنسیت بیماران
-
در دادهها، ۱۰۴ نفر مرد (۵۲٪) و ۹۶ نفر زن (۴۸٪) بودند.
-
بنابراین:
-
احتمال مرد بودن = ۰.۵۲
-
احتمال زن بودن = ۰.۴۸
-
احتمال همیشه عددی بین ۰ و ۱ است:
احتمال صفر یعنی وقوع پدیده غیرممکن است.
احتمال یک یعنی وقوع پدیده قطعی است.
هیچگاه احتمال منفی یا بزرگتر از یک وجود ندارد.
مفهوم احتمال توأم (Joint Probability)
گاهی میخواهیم احتمال وقوع همزمان دو رویداد را بررسی کنیم. این همان احتمال توأم یا Joint Probability است.
مثال: داروی Y و جنسیت
-
رویداد A = تجویز داروی Y (۹۱ نفر از ۲۰۰).
-
رویداد B = مرد بودن (۱۰۴ نفر از ۲۰۰).
-
اشتراک A و B: بیمارانی که هم مرد بودند و هم داروی Y دریافت کردند. این تعداد ۴۴ نفر از ۲۰۰ نفر است.
-
احتمال توأم = ۲۲٪.
-
-
برای زنان نیز، ۴۷ نفر از ۲۰۰ نفر داروی Y دریافت کرده بودند:
-
احتمال توأم = ۲۳.۵٪.
-
ارتقای مدل با احتمال توأم
در مدل اولیه صرفاً داروی Y بیشترین احتمال را داشت. اما اکنون با اطلاع از جنسیت، میتوانیم دقیقتر پیشبینی کنیم.
-
اگر بیمار مرد باشد، احتمالها را برای هر دارو مشروط به مرد بودن محاسبه میکنیم.
-
اگر بیمار زن باشد، همین کار را برای زنان انجام میدهیم.
این کار باعث ارتقای مدل و افزایش دقت پیشبینی میشود.
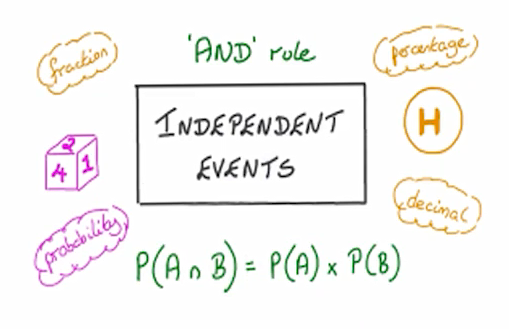
قانون استقلال رویدادها
اگر دو رویداد مستقل از یکدیگر باشند، احتمال توأم آنها برابر است با حاصلضرب احتمالهایشان:
مثال
-
احتمال تجویز Y = ۰.۴۵
-
احتمال مرد بودن = ۰.۵۲
-
حاصلضرب این دو = ۰.۲۳۴ (تقریباً برابر با ۰.۲۲ مشاهدهشده).
این نشان میدهد که در این دادهها، جنسیت و داروی Y تقریباً مستقل از هم هستند.