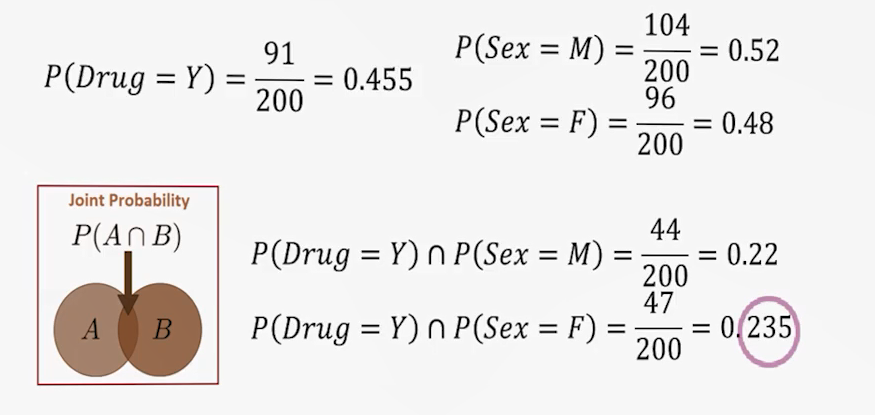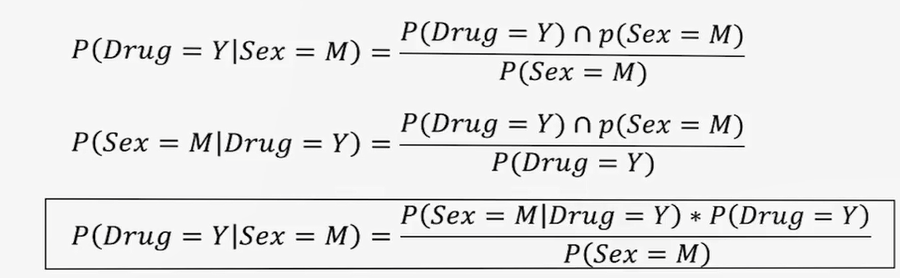در این ویدیو موضوع «قاعده یا قضیه بیز» مورد بحث قرار میگیرد. این مبحث، یکی از مفاهیم بسیار مهم و کلیدی در حوزهی احتمال و مبانی آمار است. قضیهی بیز کاربرد گستردهای در بخشهای مختلفی مانند یادگیری ماشین، مدلسازی آماری و بهطور کلی مباحث مربوط به «عدم قطعیت» دارد. هدف این جلسه، آشنایی با ایدهی اصلی قضیهی بیز و بررسی اهمیت آن در رفع برخی از چالشهای احتمالاتی است.
مروری بر مبانی احتمال
برای درک بهتر موضوع، ابتدا باید مروری بر مباحث پیشین داشته باشیم.
ما احتمال را بهعنوان «نسبت فراوانی» تعریف کرده بودیم. بهعنوان نمونه، فرض کنید در یک مجموعه داده یا فضای نمونه شامل ۲۰۰ بیمار، تعداد ۹۱ نفر داروی Y را دریافت کردهاند. در این حالت میگفتیم احتمال تجویز داروی Y برابر با ۴۵ درصد است. این تعریف، همان برداشت ما از احتمال بر اساس دادههای گذشته (Historical Data) است.
هدف ما معمولاً این است که بر مبنای دادههای گذشته، احتمال وقوع رویدادها در آینده را تخمین بزنیم. برای بهبود این تخمینها یاد گرفتیم که میتوانیم از متغیرها و رویدادهای دیگر نیز استفاده کنیم و بررسی خود را به یک متغیر محدود نکنیم.
بهعنوان مثال، اگر در همان مجموعه داده، تجویز داروی Y را در گروه مردان در نظر بگیریم، مشاهده میکنیم که از ۲۰۰ نفر، تنها ۴۴ نفر مردانی بودهاند که این دارو را دریافت کردهاند. بنابراین احتمال در این حالت ۲۲ درصد میشود. این رویکرد باعث میشود به جای آنکه برای کل افراد بدون تمایز، احتمال ۴۵ درصدی اعلام کنیم، برای گروههای مختلف (مانند مردان و زنان) احتمالهای جداگانه و دقیقتری داشته باشیم.
این محاسبات را میتوان برای متغیرهای دیگر (مانند سطح کلسترول و غیره) نیز انجام داد. در نتیجه، مجموعهای از قوانین احتمالی استخراج میکنیم که امکان تخمین دقیقتر رویدادها برای هر فرد جدید را فراهم میکند. این همان رویکردی است که در مدلهای مولد (Generative Models) مورد استفاده قرار میگیرد، زیرا اساس آن بر محاسبهی توزیعهای توأم متغیرها است.
چالشهای توزیعهای توأم
اما این روش با مشکلاتی مواجه است. یکی از مهمترین مشکلات، کمبود داده در برخی ترکیبها است. بهعنوان نمونه، اگر تنها یک یا دو رکورد در یک ترکیب خاص وجود داشته باشد، احتمال به دست آمده بسیار کوچک و نزدیک به صفر میشود و تخمین معتبری نخواهد بود. بنابراین برای محاسبهی دقیق توزیعهای توأم، نیاز به دادههای بسیار زیاد داریم؛ امری که همیشه امکانپذیر یا مقرونبهصرفه نیست.
ورود احتمال شرطی
برای حل این مشکل، مفهوم «احتمال شرطی» مطرح شد. در این رویکرد، به جای محاسبهی احتمال در کل فضای نمونه، محاسبات را محدود به زیرمجموعهها یا زیرفضاها میکنیم. مثلاً احتمال تجویز داروی Y را فقط در میان مردان محاسبه میکنیم. این کار هم هزینهی محاسباتی را کاهش میدهد و هم تمرکز را روی مسئلهی خاص مورد نظر قرار میدهد.
اما همچنان این روش نیز بینقص نیست؛ زیرا اگر دادههای مربوط به ترکیبهای خاص اندک باشند، باز هم مشکل برآورد ضعیف و غیرواقعبینانه باقی میماند.
معرفی قضیهی بیز
اینجاست که قضیهی بیز وارد عمل میشود. قضیهی بیز بهویژه در شرایطی که دادهها اندک هستند، یک راهکار مؤثر ارائه میدهد. این قضیه با تغییر در فرمول احتمال شرطی، ما را از نیاز به محاسبهی مستقیم احتمالهای توأم بینیاز میکند و امکان برآورد واقعبینانهتری را فراهم میسازد.
بهطور مشخص، اگر بخواهیم احتمال YY به شرط MM (مثلاً احتمال تجویز داروی Y برای مردان) را محاسبه کنیم، طبق تعریف احتمال شرطی باید نسبت تعداد مردانی که داروی Y دریافت کردهاند به کل بیماران محاسبه شود. مشکل این است که اگر تعداد این افراد کم باشد، تخمین نادرست خواهد بود.
اما قضیهی بیز این فرمول را بازنویسی میکند که این بازنویسی باعث میشود به جای محاسبهی احتمال توأم، از ضرب «احتمال شرطی معکوس» و «احتمال پیشین» استفاده کنیم.
به این ترتیب، قضیهی بیز امکانی فراهم میکند که با هر مشاهده یا شواهد جدید، احتمال پیشین بهروز (آپدیت) شود و یک «احتمال پسین» (Posterior Probability) محاسبه گردد.
مفهوم بهروزرسانی احتمال پیشین بر اساس شواهد جدید، هستهی اصلی قضیهی بیز است. این ویژگی در بسیاری از زمینهها، از جمله یادگیری ماشین، مدلسازی آماری و پردازش دادههای پویا (Dynamic Processes) بسیار کاربرد دارد. بهویژه در شرایطی که دادهها محدود هستند، قضیهی بیز یک ابزار قدرتمند برای برآورد احتمال محسوب میشود.