موضوع دیگری که در ادامه مباحث مربوط به تئوری احتمال میخواهیم در مورد آن صحبت کنیم، مربوط به توزیع احتمال و بحث مربوط به متغیر تصادفی است.
متغیر تصادفی
متغیر تصادفی چیز عجیب و غریبی نیست. تکتک آن ویژگیها (Features) که شما در یک دیتاست دارید، یک متغیر تصادفی هستند. به عنوان مثال:
- در دادههای مربوط به دارو، از بین چند پیشامد ممکن (مثلاً پنج نوع دارو)، هر رکورد به عنوان یک آزمایش تصادفی میتواند یکی از این مقادیر را به خود اختصاص دهد. ممکن است یک رکورد مربوط به داروی X باشد، رکورد بعدی داروی Y باشد و به همین ترتیب ادامه یابد.
- همین موضوع دربارهی جنسیت، میزان سدیم، پتاسیم، سن و سایر متغیرها نیز برقرار است.
با توجه به نوع دادهها (کمی یا کیفی)، متغیر تصادفی نیز به همین شکل تقسیمبندی میشود:
- متغیر تصادفی کیفی مانند جنسیت یا نوع دارو.
- متغیر تصادفی کمی مانند سن، قد یا میزان کلسترول.
به عنوان مثال، در دادههای مربوط به جنسیت، اگر ۴۸ درصد دادهها مربوط به خانمها و ۵۲ درصد مربوط به آقایان باشند، احتمال زن بودن برابر با ۰.۴۸ و احتمال مرد بودن برابر با ۰.۵۲ خواهد بود.
هیستوگرام و نمایش دادهها
برای دادههای کمی مانند سن، میتوان از هیستوگرام استفاده کرد. هیستوگرام دادهها را از حداقل تا حداکثر به بازههای مساوی تقسیم کرده و فراوانی هر بازه را نشان میدهد.
به طور مثال:
- اگر بازهها از ۱۶ سال شروع شود (۱۶ تا ۱۸، ۱۸ تا ۲۰، ۲۰ تا ۲۲ و …)، در هر بازه تعداد رکوردها شمارش میشود.
- نسبت هر بازه به کل دادهها (مثلاً ۷ تقسیم بر ۲۰۰) احتمال قرار گرفتن در آن بازه را نشان میدهد.
مفهوم توزیع احتمال
پس، توزیع احتمال در واقع نشان میدهد که احتمال وقوع مقادیر متغیر تصادفی چگونه در فضای نمونهها پخش شده است.
- در متغیرهای کیفی: مانند مثال جنسیت، توزیع احتمال نشان میدهد که چه بخشی از احتمال به مردان و چه بخشی به زنان تعلق دارد.
- در متغیرهای کمی: توزیع احتمال توسط نمودارهایی مانند هیستوگرام یا توابع استاندارد نمایش داده میشود.
تمرکز بیشتر احتمال در یک بازه به معنای تراکم و چگالی بالاتر در همان محدوده است و احتمال کمتر به معنای شانس کمتر وقوع در آن بازه.
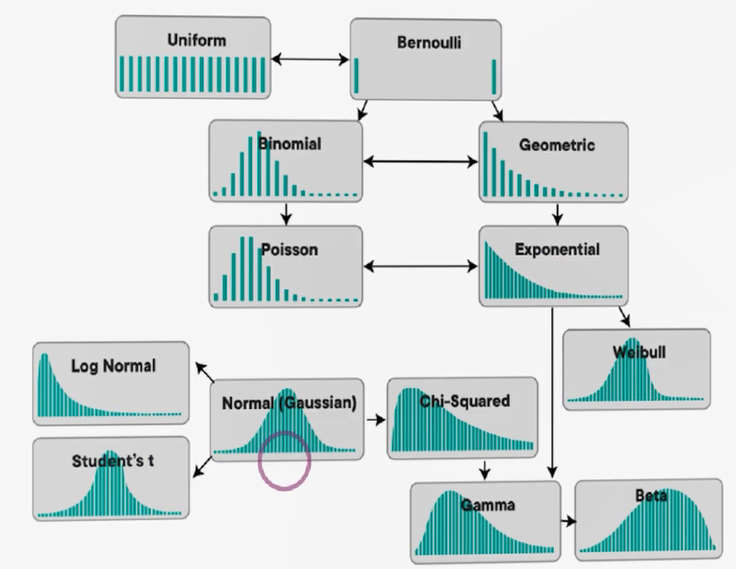
توزیعهای استاندارد
برای اینکه بتوانیم از این مفاهیم استفاده کنیم، در علم آمار توزیعهای استانداردی تعریف شدهاند. این توزیعها الگوهای شناختهشدهای هستند که احتمالها بر اساس آنها مدلسازی میشوند.
برخی از این توزیعها عبارتاند از:
- توزیع یکنواخت (Uniform): همه مقادیر در بازه مینیمم تا ماکسیمم شانس یکسانی دارند.
- توزیع نرمال (Normal): شکل زنگولهای دارد و در مرکز (میانگین) بیشترین احتمال متمرکز است.
- توزیع نمایی (Exponential)، بتا (Beta)، گاما (Gamma)، تی-استیودنت (Student’s t)، کایدو (Chi-Square)، F و بسیاری دیگر.
این توزیعها مانند شابلون عمل میکنند. تحلیلگر داده تلاش میکند ببیند کدامیک از این شابلونها بهتر با دادههای واقعی فیت (Fit) میشوند.
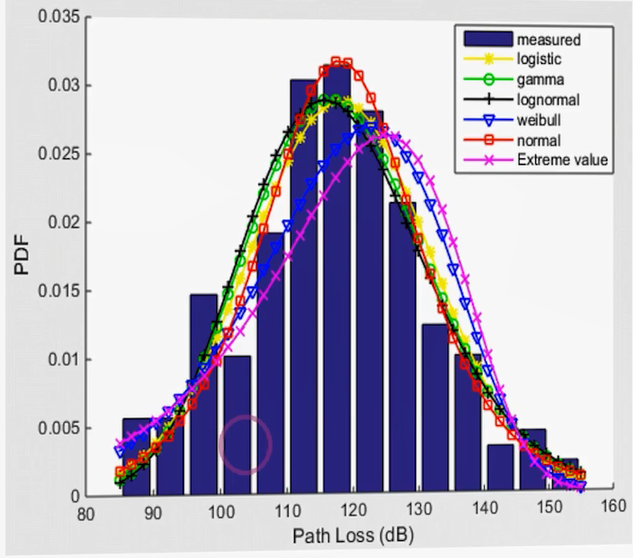
فیت کردن توزیعها روی داده
مثلاً اگر دادهها به شکل هیستوگرام نمایش داده شوند، میتوان چندین توزیع استاندارد مختلف (مانند نرمال، لوجستیک، گاما، وایبل و …) روی آن فیت کرد و سپس بررسی کرد که کدامیک بهتر دادهها را پوشش میدهد.
گاهی چند توزیع مختلف ممکن است مناسب باشند. در این حالت، روشهای آماری (مانند روش درستنمایی یا Maximum Likelihood) برای انتخاب بهترین توزیع استفاده میشوند.
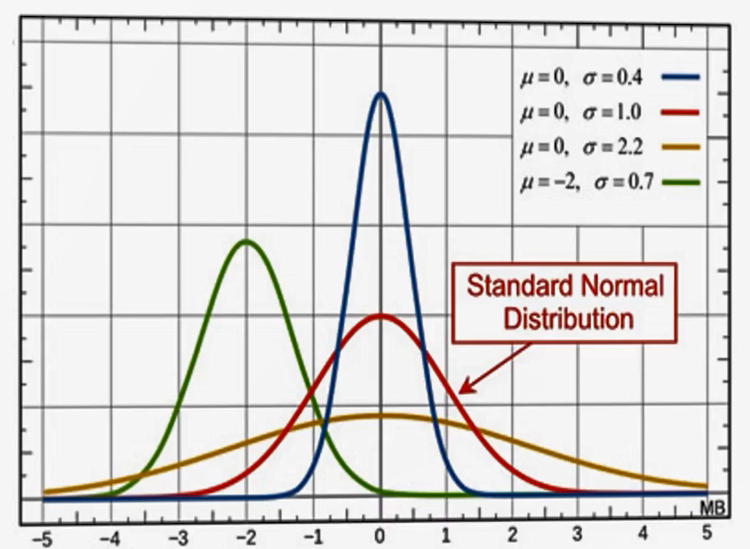
توزیع نرمال و ویژگیهای آن
توزیع نرمال یکی از پرکاربردترین توزیعهاست. ویژگیهای آن:
- متقارن است.
- میانگین و انحراف معیار (μ و σ) پارامترهای اصلی آن هستند.
- تغییر در انحراف معیار باعث تغییر در پهنای توزیع میشود:
- انحراف معیار بزرگتر: توزیع پهنتر و قله پایینتر.
- انحراف معیار کوچکتر: توزیع باریکتر و قله بلندتر.
نسخهی خاصی از این توزیع با میانگین صفر و انحراف معیار یک، توزیع نرمال استاندارد نامیده میشود.
تابع ریاضی مربوط به توزیع نرمال، تابع چگالی احتمال (PDF) نام دارد.
کاربردهای توزیع احتمال
کاربردهای توزیع احتمال بسیار متنوع است:
- در تحلیل دادهها: تشخیص دادههای پرت، مقیاسسازی، انتخاب ویژگی و کاهش ابعاد.
- در مدلسازی آماری: بسیاری از روشها فرض میکنند دادهها دارای توزیع نرمال هستند.
- در استنتاج آماری: تعمیم نتایج نمونه به جامعه.
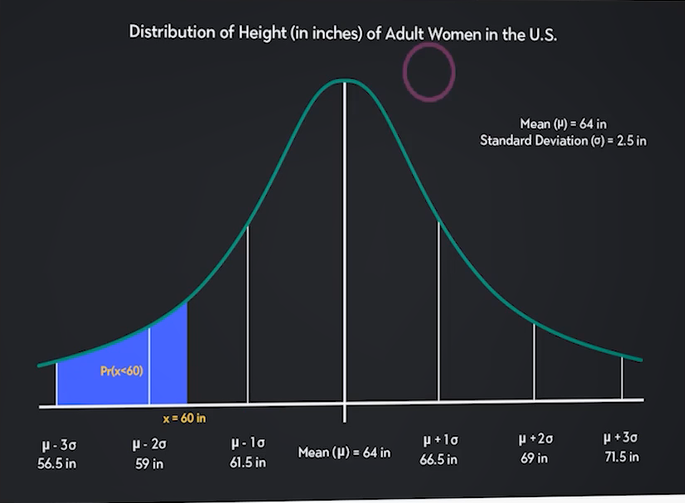
- مثال: قد زنان در آمریکا که تقریباً توزیع نرمال دارد. با دانستن میانگین و انحراف معیار، میتوان تخمین زد چه درصدی از زنان در بازههای قدی مشخص قرار میگیرند.
بنابراین، مفهوم توزیع احتمال این است که احتمال وقوع مقادیر چگونه در فضای نمونهها پخش میشود.
- برای نمایش توزیع احتمال، از شابلونهای استانداردی مانند نرمال، تی، کایدو و F استفاده میکنیم.
- این توزیعها به ما امکان میدهند تا دادههای واقعی را مدلسازی کرده و از آنها در تحلیل و تصمیمگیری استفاده کنیم.