قضیه ی بیز احتمال رخ دادن یک پیشامد را هنگامی که پیشامد دیگر اتفاق افتاده باشد، بدست میآورد. همانطور که در معادله ی زیر مشاهده می کنید، با استفاده از تئوری بیز ،خواهیم توانست احتمال رخ دادن A را هنگامی که B اتفاق افتاده باشد، بدست آوریم. در اینجا، B شواهد و A فرضیه است.

● P(A) احتمال پیشین A است(احتمال پیشین ، یعنی احتمال وقوع یک پیشامد قبل از مشاهده ی شواهد). شواهد یاevidence ، ارزش ویژگی یک نمونه ناشناخته است (در اینجا این رخ داد B است).
● P(A|B) احتمال پسین B است که به معنی احتمال وقوع حادثه پس از مشاهده شواهد(evidence) می باشد.
بیز ساده (Naive Bayes) یک الگوریتم طبقهبندی ساده اما مؤثر و متداول یادگیری ماشین (Machine Learning) است که در دستهی یادگیری با ناظر (Supervised Learning) جای میگیرد. بیز ساده الگوریتمی احتمالی است که براساس نظریهی بیز برای طبقهبندی استفاده میشود.
فرض کنید در حال قدمزدن در یک پارک هستید و جسمی قرمز در مقابل خود مشاهده میکنید. این جسم قرمز میتواند چوبدستی، خرگوش یا توپ باشد؟ شما قطعاً فرض میکنید که آن جسم یک توپ است. چرا؟
بیایید تصور کنیم که در حال ساخت ماشینی هستیم که وظیفهاش طبقهبندی یک جسم میان سه گروه چوبدستی، توپ و خرگوش است. در ابتدا احتمالاً به این فکر میکنیم که ماشینی که میسازیم بتواند ویژگیهای جسم را شناسایی کند و سپس آن را با یکی از گروههایی که میخواهیم در آنها طبقهبندی کنیم مطابقت دهد.

بهطوری که مثلاً اگر جسم دایرهای شکل باشد، پیشبینی کند که یک توپ است یا اگر آن جسم یک موجود زنده باشد، آنگاه پیشبینی ماشین ما خرگوش باشد، یا در مثالی که داشتیم، اگر جسم قرمز باشد، بهاحتمال زیاد آن را توپ در نظر بگیرد.
چرا؟ زیرا از دورهی کودکی ما توپهای قرمز زیادی دیدهایم، اما یک خرگوش قرمز یا یک چوبدستی قرمز در نظر ما بسیار بعید است.
بنابراین در مثالی که داریم ویژگی ما رنگ قرمز است که آن را با هر سه گروه مطابقت میدهیم و میبینیم که احتمال اینکه این جسم یک توپ باشد خیلی بیشتر است.

این تعریف ساده الگوریتم بیز ساده (Naïve Bayes) است. در ادامه بهصورت دقیقتر این الگوریتم را تعریف میکنیم و با مثالی آن را بهتر درک توضیح خواهیم داد.
بیز ساده (Naïve Bayes) چیست؟
بیز ساده (Naive Bayes) سادهترین الگوریتم یادگیری ماشین است که میتوانیم روی دادههای خود اعمال کنیم. همانطور که از نامش پیداست، این الگوریتم فرض میکند همهی متغیرهای مجموعهی دادهی ساده (Naïve) هستند، یعنی با یکدیگر ارتباط ندارند.
این الگوریتم از نظریهی بیز استفاده میکند که فرمول آن بهاین شکل است:

که در آن:
- c نشاندهندهی کلاس مدنظر است؛ مثلاً در مثالی که داشتیم کلاسها خرگوش و چوبدستی و توپ هستند.
- x، نشاندهندهی ویژگیهاست که هر یک بهطور جداگانه باید محاسبه شوند.
- P(c | x) احتمال پسین (Posterior) کلاس c با داشتن پیشبینیکنندهی (ویژگی) x است.
- P(c) احتمال کلاس است.
- P(x | c) معیار درستنمایی (Likelihood) است که احتمال پیشبینیکنندهی x با داشتن کلاس c را نشان میدهد.
- P(x) احتمال پیشین (Prior) پیشبینیکنندهی x است.
برای اینکه بتوانیم از این فرمول و نحوهی استفاده از آن درک بهتری داشته باشیم، در بخش بعد مثالی را با هم بررسی میکنیم.
درک بیز ساده با یک مثال
مجموعهدادهای داریم که شرایط آبوهوایی برای بازی گلف را شرح میدهد. با توجه به شرایط آبوهوایی شرایط برای بازی گلف مناسب (بله) یا نامناسب (خیر) طبقهبندی میشود.
ما در اینجا ۴ ویژگی داریم که اولی آبوهوا (Outlook) است که میتواند بارانی (Rainy)، آفتابی (Sunny) و ابری (Overcast) باشد. دومی دما (Temperature) است که گرم (Hot)، معتدل (Mild) و یا خنک (Cool) میتواند باشد.
ویژگی بعدی رطوبت (Humidity) است که دو حالت نرمال (Normal) و بالا (High) را دربرمیگیرد. ویژگی آخر هم باد (Windy) است که میتواند بادی باشد (True) یا بادی نباشد (False) باشد.

در اینجا احتمال بازیکردن از بین چهارده دادهای که داریم، P (Yes) = 9/14 است و احتمال بازینکردن میان این چهارده داده P (No) = 5/14 است. حال باید احتمالات جداگانهی مرتبط با هر ویژگی، یعنی دما (Temperature)، رطوبت (Humidity)، باد (Windy) و شرایط آبوهوا (Outlook)، را محاسبه کنیم.

حال فرض کنید باید نمونهی جدید X را طبقهبندی کنیم که اطلاعات آن بهاین شرح است:
- Outlook = sunny
- Temperature = cool
- Humidity = high
- Wind = true
یعنی هوا آفتابی، دما خنک، رطوبت زیاد و باد هم وجود دارد.
بنابراین احتمال بازی گلف بهاین شرح است:
برای شرایطی که این داده جدید دارد هم احتمال بازیکردن و هم احتمال بازینکردن را از روی جدول بالا بار دیگر مینویسیم:
- P(outlook =sunny | play = yes) = 2/9
- P(temperature=cool | play = yes) = 3/9
- P(Humidity = high | play = yes) = 3/9
- P(wind = true | play = yes) = 3/9
- P(play = yes) = 9/14
- P(outlook =sunny | play = no) = 3/5
- P(temperature=cool | play = no) = 1/5
- P(Humidity = high | play = no) = 4/5
- P(wind = true | play = no) = 3/5
- P(play = no) = 5/14
احتمال انجامدادن بازی گلف براساس الگوریتم بیز ساده (Naïve Bayes)
حال با توجه به فرمول بیز ساده، اول احتمال این را که بازی صورت گیرد یا نگیرد برای این دادهی جدید، یعنی X، محاسبه میکنیم.
بهاین صورت که یک بار احتمال هر یک از ویژگیها (باد، رطوبت، دما، هوا) را برای صورتگرفتن بازی که در بالا هم بار دیگر از روی جدول برای راحتی کار نوشتیم و احتمال P (Yes) = 9/14، در هم ضرب میکنیم؛ سپس بار دیگر بار احتمال هر یک از ویژگیها (باد، رطوبت، دما، هوا) را برای صورتنگرفتن بازی و احتمال P (No) = 5/14 در هم ضرب میکنیم:

P(X | play = yes).P(play = yes) = 2/9 * 3/9 * 3/9 * 3/9 * 9/14 = 0.0053
3/5 × 1/5 × 4/5 × 3/5 × 5/14 = 0.0206 = (P(X | play = no).P(play = no))
حال که مقدار P (c) P (c | x). را داریم، باید اول مقدار P(X) را به دست آوریم و درنهایت طبق فرمول بیز، P (c) P (c | x). را بر P(X) تقسیم کنیم:

P(X) = 0.0053 + 0.0206 = 0.0259
P(play = Yes | X) = (P(X | play = yes).P(play = yes)) / P(X) = 0.204
P(play = No | X) = (P(X | play = no).P(play = no)) / P(X) = 0.806
این یعنی با احتمال 0.806، پیشبینی ما در مورد بازی گلف «نه» است؛ یعنی بازی صورت نمیگیرد.
مروری بر مفاهیم تئوری احتمال
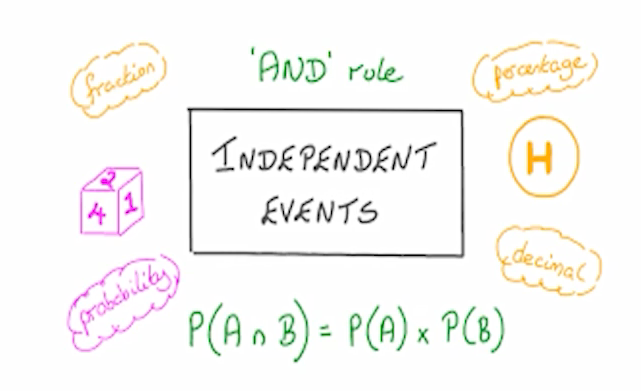
پیشامدهای مستقل و قانون ضرب احتمال
وقتی وقوع پیشامد مستقل از وقوع پیشامد دیگری باشد، احتمال وقوع همزمان آنها برابر با حاصل ضرب احتمال هر یک از پیشامدها می باشد.
احتمال شرطی
در بسیاری از مواقعی که بین وقوع دو پیشامد استقلال وجود نداشته باشد، میتوان با آگاهی از نتیجه پیشامد اول، احتمال وقوع پیشامد دوم را در فضای نمونه کوچکتری جستجو کرد و مقدار احتمال را محاسبه نمود.

قانون احتمال کل
احتمال یک پیشامد را می توان به صورت حاصل جمع احتمال های شرطی آن در افراز پیشامد دیگری بازنویسی کرد.


قانون بیز
محاسبه احتمال شرطی بدون نیاز به محاسبه احتمال توأم دو پیشامد در بسیاری از موارد به سادگی قابل محاسبه نیست.
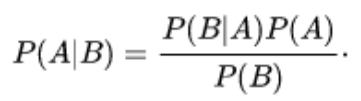
بسط قانون بیز بر اساس قانون احتمال کل
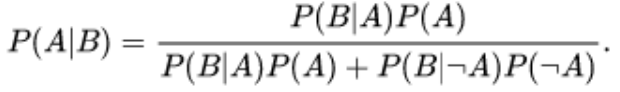
الگوریتم بیز ساده
این الگوریتم یک مدل رده بندی احتمالاتی تولید کرده و بر اساس مشاهدات مربوط به داده های ورودی، مقداری از فیلد هدف را که دارای بیشترین احتمال وقوع باشد را بر می گرداند.
الگوریتم بیز ساده یکی از انواع الگوریتم های یادگیری با نظارت از نوع رده بندی برای فیلد هدف کیفی میباشد. فرض کنید بر اساس ویژگی ورودی x به دنبال محاسبه احتمال وقوع فیلد هدف y هستیم. بنابراین بر اساس قانون بیز رابطه روبرو را خواهیم داشت:
Posterior = Likelihood * Prior / Evidence

استفاده از الگوریتم رده بندی بیز ساده در شرایط واقعی، شامل مشاهدات چند بعدی 𝑛𝑥,…, 𝑥𝑖 = 𝑥1,𝑥2می باشد. این الگوریتم، با در نظر گرفتن فرض قوی استقلال بین بردارهای ورودی و استفاده از قانون ضرب احتمال و قانون احتمال کل، محاسبه قانون بیز را به صورت زیر انجام می دهد

محاسبه بیشینه احتمال پسین: Maximum a Posterior (MAP)
پیش بینی برچسب فیلد هدف با محاسبه احتمال وقوع هر یک از کلاس ها، به شرط مقادیر ویژگی های ورودی و تعیین کلاسی که مقدار احتمال را بیشینه کند (MAP)انجام می پذیرد.
فرض کنید فیلد هدف به تعداد K کلاس دارد؛ در اینصورت پیش بینی برچسب کلاس فیلد هدف بر اساس رابطه زیر بدست می آید.

- مقداری از کلاس فیلد هدف 𝑐𝑘 به عنوان رده پیش بینی شده انتخاب می گردد، که مقدار تابع رده بند بیز را بیشینه کند.
ویژگی های الگوریتم بیز ساده (Naïve Bayes)
به علت فرض استقلال بین ویژگی های ورودی، محاسبه رابطه بیز با جداسازی توزیع احتمال شرطی برای هر ویژگی بصورت مستقل از سایر ویژگی ها انجام می شود و این موضوع دو نتیجه مهم در پی خواهد داشت:
- نسبت به بسیاری از الگوریتم های دیگر رده بندی، نیاز به داده های کمتری برای محاسبات خود دارد و از این رو یکی از کاندیداهای مناسب برای مواقعی که با داده های کم مواجه هستیم می باشد.
- هرچند با ساده سازی روابط بین ویژگی های ورودی، مقدار احتمال پسین بدست آمده اغلب دارای خطا و انحراف از مقدار واقعی می باشد، اما با توجه به نحوه تخصیص برچسب کلاس هدف بر اساس ،MAP فارغ از اینکه برآورد احتمال کم یا زیاد دارای خطا باشد، اما برچسب پیش بینی شده به درستی گزینه محتمل تری نسبت به سایر مقادیر است.
به علت فرض استقلال بین ویژگی های ورودی، محاسبه رابطه بیز با جداسازی توزیع احتمال شرطی برای هر ویژگی بصورت مستقل از سایر ویژگی ها انجام می شود و این موضوع دو نتیجه مهم در پی خواهد داشت:
- به علت محاسبات بسیار سریع، در مسائلی که نیاز به پیش بینی بلادرنگ (Real Time) و یا در شرایط وجود داده های با حجم بسیار زیاد، گزینه مطلوبی هست.
- به علت پشتیبانی کامل از فیلد هدف چند کلاسه و محاسبه احتمال پسین برای هر کلاس (روش،)MAP در اغلب مسائل رده بندی مانند رده بندی متون) ،(Text Classification تشخیص اسپم (Spam Filtering) تحلیل احساسات در شبکه های اجتماعی Analysis) (Sentiment و سیستم های پیشنهاد دهنده (Recommendation System) بسیار مورد توجه می باشد.
مثال:استفاده از الگوریتم بیز ساده در تشخیص اسپم
فرض کنید داده های آموزشی در دسترس شامل 6 متن ایمیل مطابق جدول روبرو است که با برچسب های “ham” و “spam” کلاس آنها مشخص شده است. می خواهیم با استفاده از الگوریتم بیز ساده، برچسب ایمیل جدید با متن ” review us now“ را تشخیص دهیم:

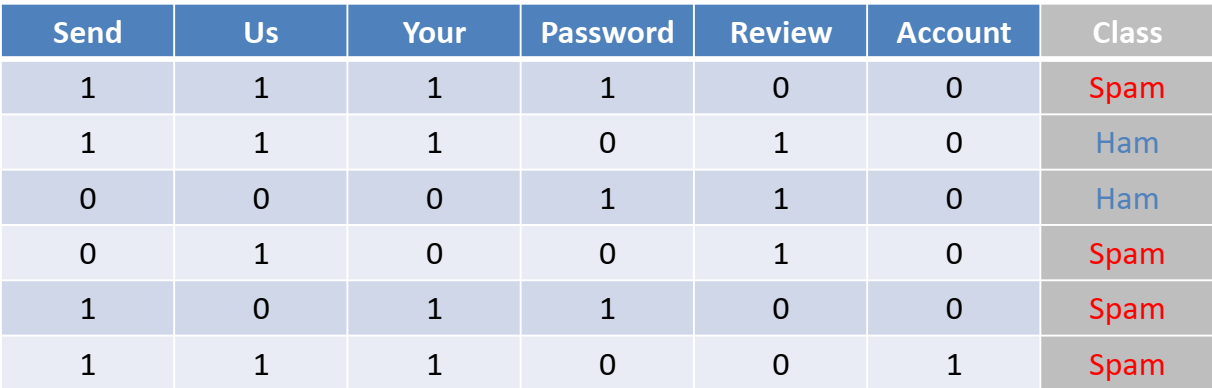
بر اساس روابط بیز، احتمال پیشین کلاس های هدف و همچنین احتمال پسین به شرط وقوع یک ویژگی با کمک داده های آموزشی بدست می آید:

برای استفاده از رده بند بیز ساده، بایستی محاسبات قانون بیز به صورت جداگانه برای هر ویژگی و همچنین به تفکیک کلاس های فیلد هدف انجام شود. در جدول زیر محاسبه مقدار درست نمایی تمام ویژگی های مورد بررسی به تفکیک دو کلاس نشان داده شده است:
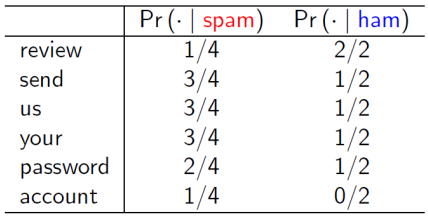
محاسبه مقدار درستنمایی برای عبارت ایمیل جدید به تفکیک کلاس های هدف انجام می شود:

در نهایت محاسبه احتمال پسین برای عبارت ایمیل جدید محاسبه می شود و با توجه به اینکه مقدار آن برای کلاس spam کوچکتر می باشد، در نتیجه با احتمال 0.877 ایمیل جدید متعلق به کلاس ham می باشد.