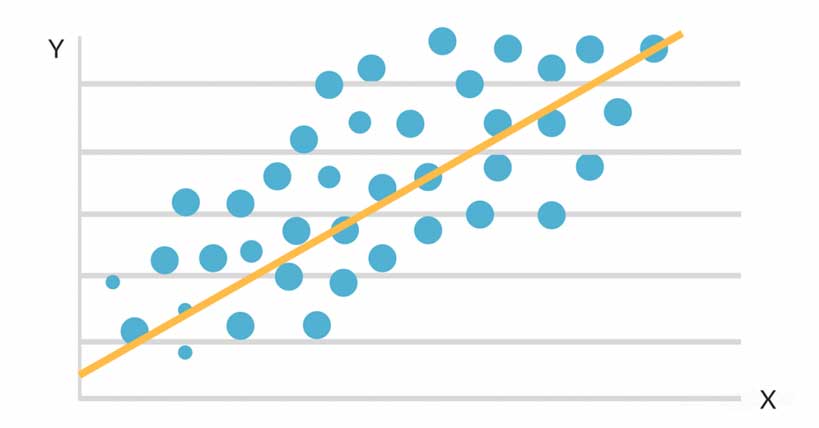
رگرسیون خطی یکی از پرکاربردترین الگوریتم های یادگیری آماری با هدف بررسی و مدلسازی ارتباط خطی بین یک یا چند ویژگی ورودی مستقل از هم با متغیر وابسته (پاسخ) می باشد. رگرسیون خطی از نوع یادگیری با نظارت با هدف پیش بینی مقادیر کمی است.
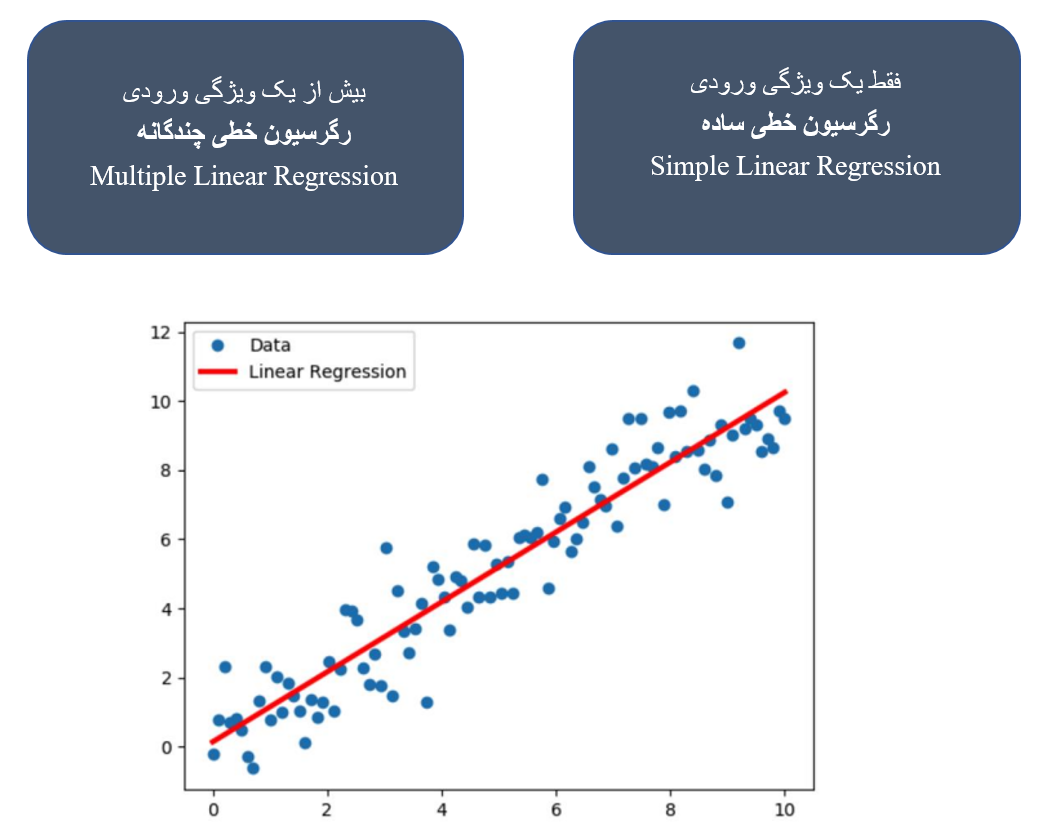
اگر رابطه خطی بین یک متغیر پاسخ و یک متغیر مستقل برقرار شود، تکنیک رگرسیون را رگرسیون خطی ساده (Simple Linear Regression) مینامند. ولی در صورت به کارگیری چندین متغیر توصیفی یا مستقل در مدل رگرسیونی، روش رگرسیونی را «چند گانه» (Multiple Linear Regression) میگویند.
البته روش رگرسیونی دیگری براساس چند متغیر پاسخ و مستقل نیز به کار گرفته میشود که به آن «رگرسیون چند متغیره» (Multivariate Regression) گفته شده و بیش از یک متغیر پاسخ مورد تحلیل و مدلسازی قرار میگیرد.
رگرسیون خطی ساده
هدف مدل رگرسیون، یافتن بهترین مقدار برای پارامترهای مدل به منظور به حداقل رساندن مجموع مجذور خطاها می باشد.
اگر برای شناسایی و پیشبینی متغیر وابسته فقط از یک متغیر مستقل استفاده شود، مدل را رگرسیون خطی ساده Simple Linear Regression میگویند. فرم مدل رگرسیون خطی ساده به صورت زیر است:
Y=β0+β1X+ϵ
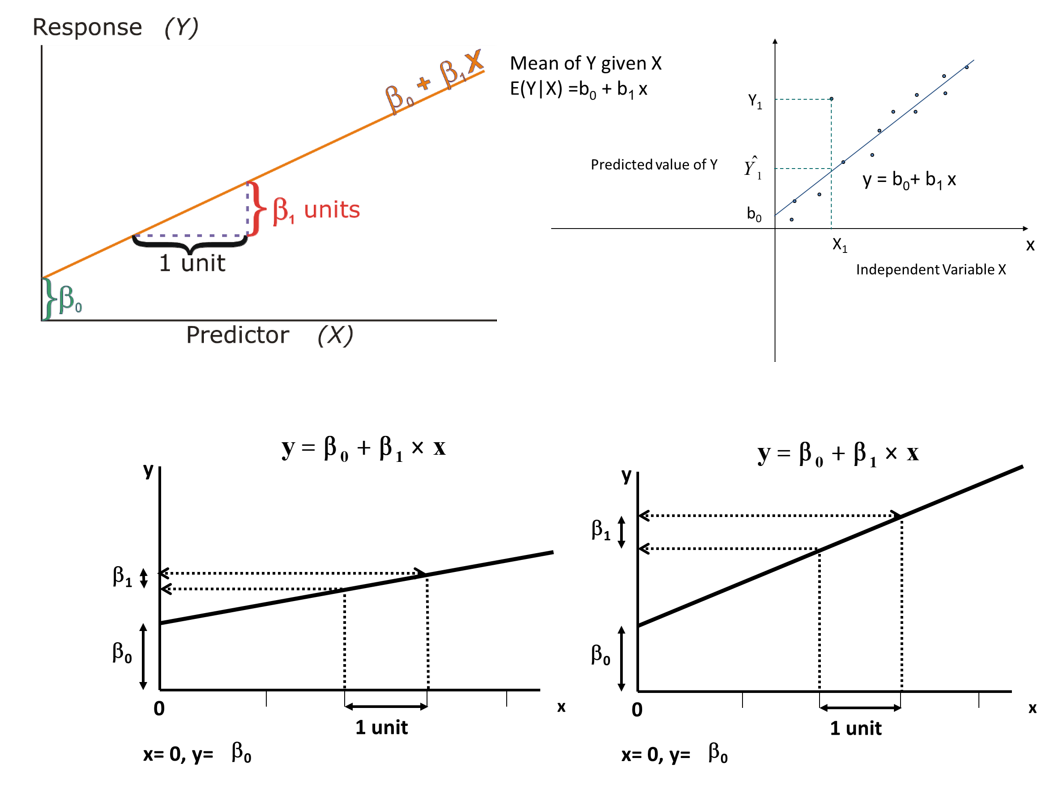
همانطور که دیده میشود این رابطه، معادله یک خط است که جمله خطا یا همان ϵϵ به آن اضافه شده. پارامترهای این مدل خطی عرض از مبدا (β0) و شیب خط (β1) است. شیب خط در حالت رگرسیون خطی ساده، نشان میدهد که میزان حساسیت متغیر وابسته به متغیر مستقل چقدر است.
به این معنی که با افزایش یک واحد به مقدار متغیر مستقل چه میزان متغیر وابسته تغییر خواهد کرد. عرض از مبدا نیز بیانگر مقداری از متغیر وابسته است که به ازاء مقدار متغیر مستقل برابر با صفر محاسبه میشود. به شکل دیگر میتوان مقدار ثابت یا عرض از مبدا را مقدار متوسط متغیر وابسته به ازاء حذف متغیر مستقل در نظر گرفت.
برای مثال فرض کنید کارخانهای میخواهد میزان هزینههایش را براساس ساعت کار برآورد کند. شیب خط حاصل از برآورد نشان میدهد به ازای یک ساعت افزایش ساعت کاری چه میزان بر هزینههایش افزوده خواهد شد.
از طرفی عرض از مبدا خط رگرسیون نیز هزینه ثابت کارخانه حتی زمانی که ساعت کاری نیست نشان میدهد. این هزینه را میتوان هزینههای ثابت مانند دستمزد نگهبانان و هزینه روشنایی فضای کارخانه فرض کرد.
گاهی مدل رگرسیونی را بدون عرض از مبدا در نظر میگیرند و β0=0 محسوب میکنند. این کار به این معنی است که با صفر شدن مقدار متغیر مستقل، مقدار متغیر وابسته نیز باید صفر در نظر گرفته شود. زمانی که محقق مطمئن باشد که که خط رگرسیون باید از مبدا مختصات عبور کند، این گونه مدل در نظر گرفته میشود. فرم مدل رگرسیونی در این حالت به صورت زیر است:
Y=β1X+ϵY=β1X+ϵ
از آنجایی که پیشبینی رابطه بین متغیر وابسته و مستقل به شکل دقیق نیست، جمله خطا را یک «متغیر تصادفی» (Random Variable) با میانگین صفر در نظر میگیرند تا این رابطه دارای اریبی نباشد.
باید توجه داشت که منظور از رابطه خطی در مدل رگرسیون، وجود رابطه خطی بین ضرایب است نه بین متغیرهای مستقل. برای مثال این مدل y=β0+β1×2+ϵy=β0+β1×2+ϵ را نیز میتوان مدل خطی در نظر گرفت در حالیکه مدل y=β0xβ1+ϵy=β0xβ1+ϵ دیگر خطی نیست و به مدل نمایی شهرت دارد.
همچنین در فرضیات این مدل، خطا یک جمله تصادفی است و تغییرات آن مستقل از متغیر X است. به این ترتیب مقدار خطا وابسته به مقدار متغیر مستقل نیست.
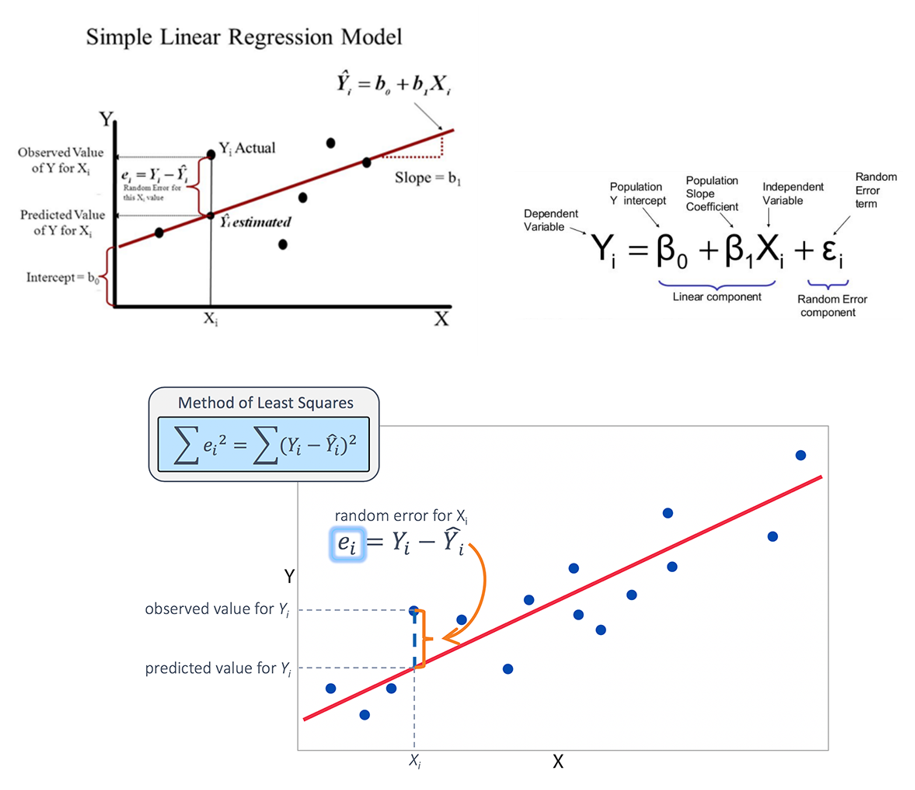
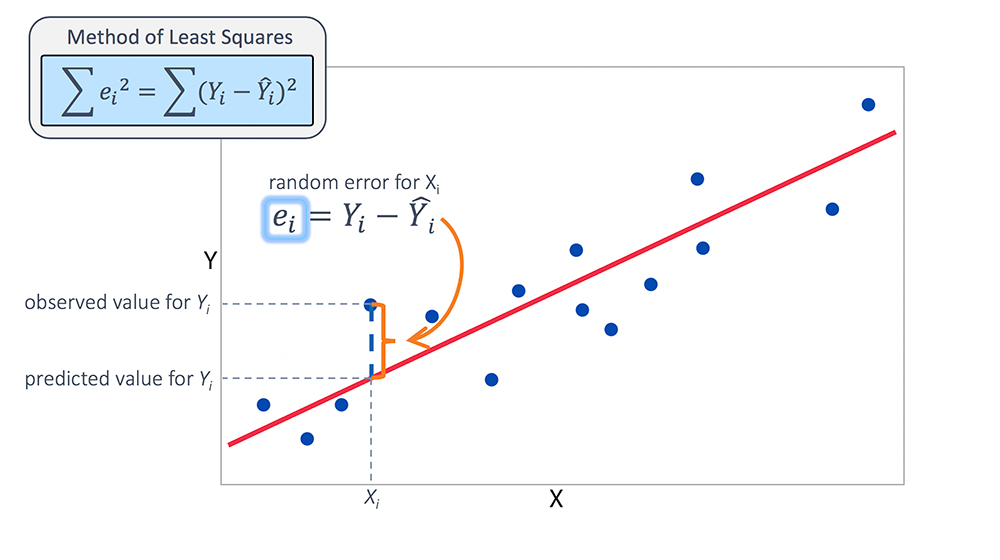
در رگرسیون خطی سعی میشود، به کمک معادله خطی که توسط روش رگرسیون معرفی میشود، برآورد مقدار متغیر وابسته به ازای مقدارهای مختلف متغیر مستقل توسط خط رگرسیون بدست آید. به منظور برآورد پارامترهای مناسب برای مدل، کوشش میشود براساس دادههای موجود، مدلی انتخاب میشود که کمترین خطا را داشته باشد.
روشهای مختلفی برای تعریف خطا و حداقل کردن آن وجود دارد. معیاری که در مدل رگرسیون خطی ساده به کار میرود، کمینه کردن مجموع مربعات خطا است. از آنجایی که میانگین مقدارهای خطا صفر در نظر گرفته شده است، میدانیم زمانی مجموع مربعات خطا، حداقل ممکن را خواهد داشت که توزیع دادهها نرمال (Normal Distribution) باشند.
در نتیجه، نرمال بودن دادههای متغیر وابسته یا باقیماندهها یکی از فرضیات مهم برای مدل رگرسیونی خطی ساده است.
رگرسیون خطی چندگانه
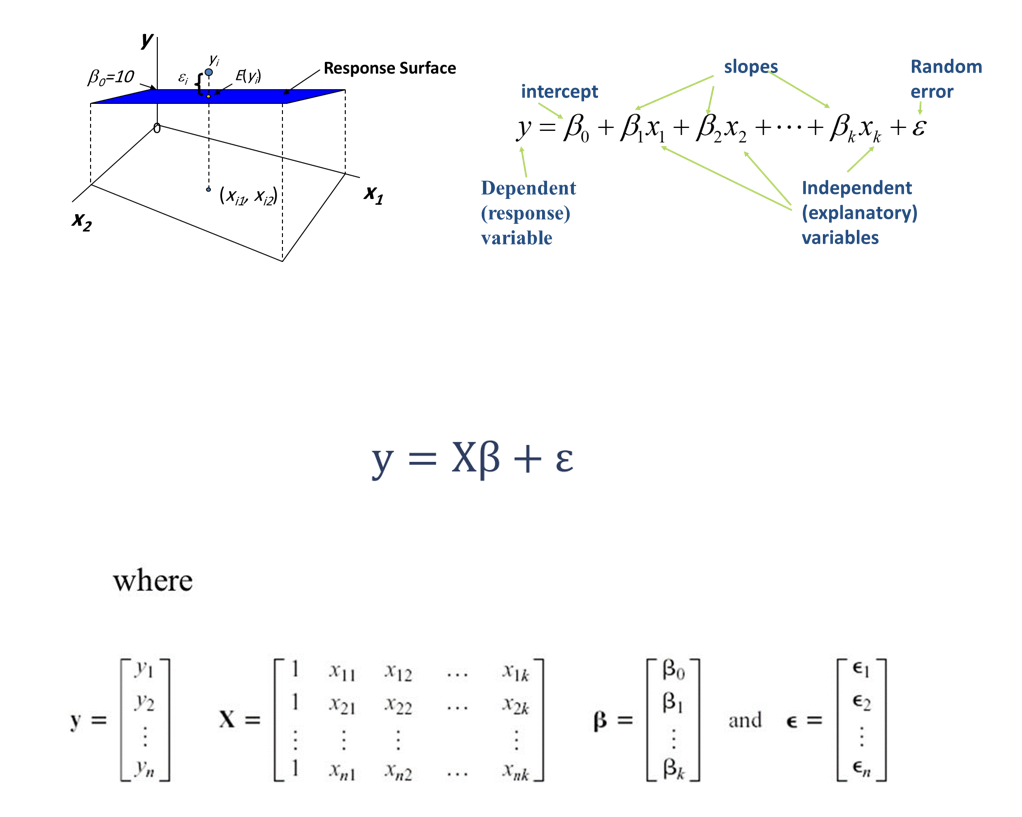
در رگرسیون خطی چندگانه، پارامترهای یک مدل خطی به کمک یک تابع هدف و مقدارهای متغیرها، برآورد میشوند. در رگرسیون خطی، مدل در نظر گرفته شده، یک رابطه خطی بر حسب پارامترهای مدل است. به این ترتیب اگر nn مشاهده از متغیر مستقل pp بعدی XX داشته باشیم و بخواهیم یک رابطه خطی با متغیر پاسخ yy برقرار کنیم، میتوانیم از مدل رگرسیون خطی زیر استفاده کنیم.
yi=β01+β1xi1+⋯+βpxip+εi,i=1,…,nyi=β01+β1xi1+⋯+βpxip+εi i=1,…,n
از آنجایی که متغیر مستقل X دارای p بعد است، مقدار آن را در هر بعد با یک متغیر مستقل یک بعدی جایگزین کردهایم. مشخص است که اندیس ii نیز شماره مشاهده را نشان میدهد. در انتها نیز ε جمله خطای مدل رگرسیونی محسوب میشود.
در رگرسیون خطی ساده، رابطه بین متغیر مستقل و وابسته به صورت معادله یک خط بیان میشود. در رگرسیون چندگانه، اگر دو متغیر مستقل با یک متغیر وابسته در رابطه خطی باشند، شکل این رابطه به صورت یک صفحه (plane) در خواهد آمد. در صورتی که بیش از دو متغیر مستقل در مدل رگرسیون خطی به کار روند، مدل به شکل یک «ابرصفحه» (Hyperplane) ظاهر میشود.