مقاله‌ی حاضر دایکه، ادامه‌ی مثال مطالعه‌ی موردی خرده‌فروشی است که چند هفته‌ی گذشته روی آن کار می‌کردیم. بخش‌های قبلی مثال مطالعه‌ی موردی را می‌توانید در لینک‌های زیر پیدا کنید:
بخش ۱: مقدمه
بخش ۲: تعریف مسئله
بخش ۳: EDA
بخش ۴: تحلیل وابستگی
بخش ۵: درخت تصمیم (CART)
اگر از مقاله‌ی قبلی یادتان باشد، الگوریتم CART درخت‌های تصمیمی تولید می‌کند که فقط گره‌های فرزند دوتایی دارند. در مقاله‌ی حاضر، الگوریتم دیگری یاد می‌گیریم تا درخت‌های تصمیمی با گره‌های فرزند چندتایی بسازیم. چندین روش برای دستیابی به این هدف موجود است، مثل CHAID (شناساگر تعامل خودکار مربع خی[1]). در اینجا، راجع به الگوریتم c4.5 می‌آموزیم تا درخت‌های تصمیمی با گره‌های فرزند چندتایی تولید کنیم. چرا که این الگوریتم از مفهومی استفاده می‌کند که به دلم نشسته است.
آنتروپی
قانون اول ترمودینامیک مربوط به تبدیل انرژی را در دبیرستان آموختیم. طبق این قانون:
انرژی نه تولید می‌شود، نه از بین می‌رود؛ به بیان دیگر، انرژی کل جهان ثابت است.
اولین واکنش بیشتر دانش‌آموزان پس از فراگیری این واقعیت این بود: پس چرا برای ذخیره‌ی الکتریسیته و سوخت خودمان را به زحمت بیندازیم؟ اگر انرژی کل جهان ثابت و محفوظ است، پس میزان نامحدودی از انرژی برای مصرف داریم که هیچ‌گاه از بین نمی‌رود.
هرچند، قانون دوم ترمودینامیک این راحتی خیال مربوط به تلف‌شدن انرژی را نابود می‌کند. آنتروپی منشأ اصلی قانون دوم ترمودینامیک است. آنتروپی میزان بی‌نظمی یا تصادفی‌بودن در جهان است. جهت کلی جهان از نظم به سوی بی‌نظمی یا تصادفی‌بودن بالاتر است. قانون دوم می‌گوید:
آنتروپی کل یا بی‌نظمی/ تصادفی‌بودن کل جهان همواره درحال افزایش است.
بسیار خُب، اجازه دهید مثالی بزنیم تا این قانون را بهتر بفهمیم. زمانی‌که برای راه‌انداختن خودروتان از سوخت استفاده می‌کنید، بنزین کاملاً منظم (انرژی فشرده) به اشکال بی‌نظمی از انرژی، مثل گرما، صوت، جنبش و غیره تبدیل می‌شود. حین این فرایند، کار تولید می‌شود تا موتور خودرو را به‌راه اندازد. هر چه این انرژی تصادفی‌تر یا بی‌نظم‌تر باشد، استخراج کاری هدف‌دار از آن دشوارتر/ ناممکن‌تر می‌شود. پس به نظرم ما به کار اهمیت می‌دهیم، نه به انرژی. به بیان دیگر، هر چه آنتروپی یا تصادفی‌بودن سیستمی بالاتر باشد، تبدیل آن به کار معنادار دشوارتر می‌شود. فیزیکدانان آنتروپی سیستم را توسط فرمول زیر تعیین می‌کنند:
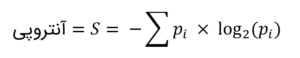
آنتروپی، اصل نظریه‌ی اطلاعات هم هست. کلاده شانون[2]، پدر نظریه‌ی اطلاعات، نبوغش را به‌کار گرفت تا روابط بین ترمودینامیک و اطلاعات را شناسایی کند. وی طی پیام خاصی، تعریف آنتروپی زیر را برای سنجش تصادفی‌بودن پیشنهاد کرد:
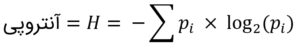
برای مثال، آنتروپی (تصادفی‌بودن) سکه‌ی سالم، با شانس یکسان شیر و خط، ۱ بیت (طبق محاسبه‌ی زیر) است. توجه داشته باشید که واحد آنتروپی در نظریه‌ی اطلاعات بیت است که توسط کلاده شانون ابداع شد. از همین واحد به‌عنوان واحد اصلی حافظه‌ی رایانه هم استفاده می‌شود.
برای ساختن درخت تصمیم و پوشیده‌خوانی اطلاعات درون داده‌ها از همین فرمول استفاده خواهیم کرد.
مثال مطالعه‌ی موردی خرده‌فروشی – درخت تصمیم (آنتروپی: الگوریتم C4.5)
به مثال مطالعه‌ی موردی خرده‌فروشی‌مان برمی‌گردیم؛ در این مثال، شما مدیر ارشد تحلیل و رئیس راهبرد کسب‌وکار فروشگاه آنلاینی به‌نام درس‌اسمارت هستید که در عرضه‌ی پوشاک تخصص دارد. در این مورد، هدفتان بهبود عملکرد کمپین آتی است. برای دستیابی به این هدف، داده‌های برگرفته از کمپین قبلی که کاتالوگ‌های کالاها را مستقیماً به صدها هزار مشتری از پایگاه مشتریان چند میلیون نفری ارسال می‌شد را تحلیل می‌کنید. نرخ واکنش کلی این کمپین ۴.۲ درصد بود.
شما کل صدها هزار مشتری متقاضی را برمبنای فعالیت‌های ۳ ماه اخیرشان، پیش از شروع کمپین، به سه دسته تقسیم کرده‌اید. جدول زیر همان جدولی است که در مقاله‌ی قبلی، به‌منظور خلق درخت تصمیم با استفاده از الگوریتم CART به‌کار بردیم.
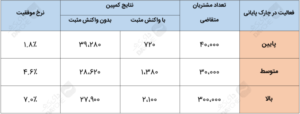
شکل زیر، درختی با گره دوتایی است که در مقاله‌ی قبلی، با استفاده از CART ساختیم.
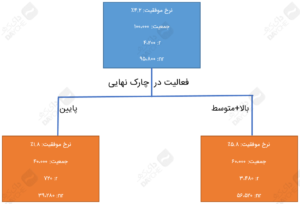
درخت تصمیم – CART
بیایید ببینیم می‌توانیم با استفاده از آنتروپی یا الگوریتم c4.5 درخت بهتری بسازیم یا نه. از آنجایی‌که الگوریتم c4.5 قادر به تولید درخت‌های تصمیمی با گره‌های چندتایی است، پس یک احتمال دیگری از درخت (با سه گره – پایین؛ متوسط؛ بالا) خواهیم داشت. این علاوه بر درخت‌هایی دوتایی است که در مقاله‌ی قبلی کاوش کردیم.
روش کار c4.5، مقایسه‌ی آنتروپی کلیه‌ی درخت‌های ممکن با داده‌های اصلی (داده‌های خط‌مبنا) است. سپس، درختی با بیشترین حصول (بازده) اطلاعاتی، یعنی اختلاف آنتروپی‌ها را انتخاب می‌کند:
بنابراین، اول باید آنتروپی خط‌مبنای داده‌هایی با ۴.۲ درصد تبدیل[3] (۴۲۰۰ مشتری تبدیل‌شده از بین ۱۰۰،۰۰۰ مشتری متقاضی) را محاسبه کنیم. توجه کنید که ۹۵.۸ درصد (۴.۲٪ – ۱۰۰٪ =) در جمله‌ی دوم، درصد مشتریان تبدیل‌نشده است.
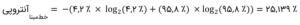
این همان مقداری است که در پایین‌ترین ردیف جدول زیر برای آنتروپی کل به‌دست آوردیم.
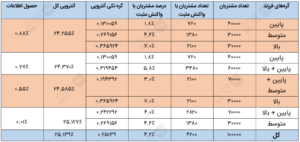
حالا بیایید با محاسبه‌ی آنتروپی‌های اجزاء تکی درخت اول (با سه گره – پایین؛ متوسط؛ بالا)، آنتروپی درخت را بیابیم.
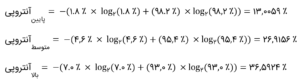
حالا آنتروپی کل این درخت، همان مجموع موزون کلیه‌ی اجزاءاش است. در اینجا، وزن‌ها، تعداد مشتریان یک گره تقسیم بر تعداد کل مشتریان هستند؛ مثلاً، ۰.۴ = ۴۰،۰۰۰/۱۰۰،۰۰۰ برای گره اول .
نهایتاً، باید مقدار حصول اطلاعات را محاسبه کنیم، یعنی:
ضمناً، حصول اطلاعات درختی با سه گره، در مقایسه با سایر درخت‌ها از همه بالاتر است (به جدول بالا نگاهی بیندازید). بنابراین، الگوریتم c4.5 با استفاده از آنتروپی، درخت تصمیم زیر را خلق می‌کند:
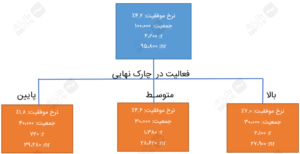
درخت تصمیم c4.5 با استفاده از آنتروپی
و اما حرف آخر
چقدر آنتروپی جالب است! بله، اعتراف می‌کنم عاشق فیزیکم. هرچند، این رابطه‌ی بین ترمودینامیک و اطلاعات هنوز هم موهای تنم را سیخ می‌کند. ایده‌ی کلی این است که اطلاعات عدم قطعیت یا تصادفی‌بودن سیستم را حذف می‌کند. پس، با استفاده از اطلاعات می‌توان مسیر را از بی‌نظمی به نظم تغییر داد! بله، سرنوشت جهان این‌طور رقم خورده است که به سوی بی‌نظمی یا تصادفی‌بودن پیش برود، اما هنوز می‌توانیم از اطلاعات برای ایجاد نظم در سیستم‌های کوچک استفاده کنیم.
تا مقاله‌ی بعدی!
[1] CHi-squared Automatic Interaction Detector
[2] Claude Shannon
[3] conversion
