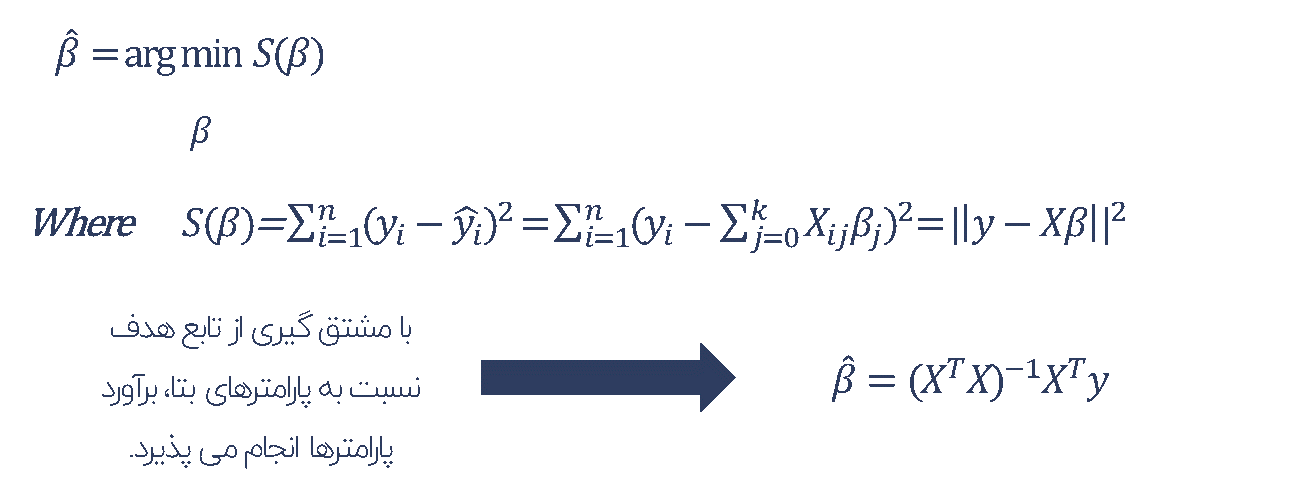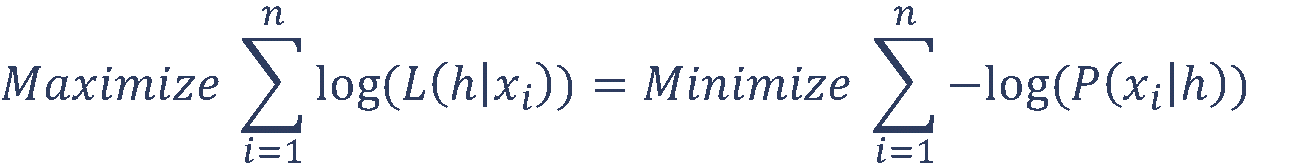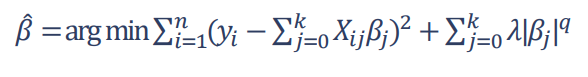روش حداقل مربعات معمولی (Ordinary Least Square Method – OLS)
این روش به عنوان رایج ترین و پرکاربردترین رویکرد در برآورد پارامترهای مدل رگرسیون مورد استفاده قرار می گیرد. برای محاسبه ضرایب مدل، با استفاده از محاسبات ماتریسی در جبر خطی بهترین مقادیر برای پارامترهای مجهول مدل به شکلی یافت می شود که مجموع مربعات خطای مدل (اختلاف بین مقدار واقعی و مقدار خط رگرسیونی) کمینه شود.
در حجم داده های زیاد، محاسبات ماتریسی لازم در این روش نیاز به دسترسی به داده های کامل و حافظه کافی (Memmory) می باشد.
روش تخمین بیشینه درستنمایی (Maximum Likelihood Estimation – MLE)
یکی از بهترین و مطمئن ترین روشهای برآورد در آمار، روش مبتنی بر تابع درستنمایی هست.
تابع درستنمایی: احتمال مشاهده نمونه های مشخصی از داده ها را، به شرط درستی یک فرضیه (مدل یا پارامترهای توزیع) درستنمایی می گویند. در صورتی که نمونه ها را ثابت در نظر بگیریم با تغییر مقدار پارامتر در فضای مربوط به آن، تابع درستنمایی را خواهیم داشت.
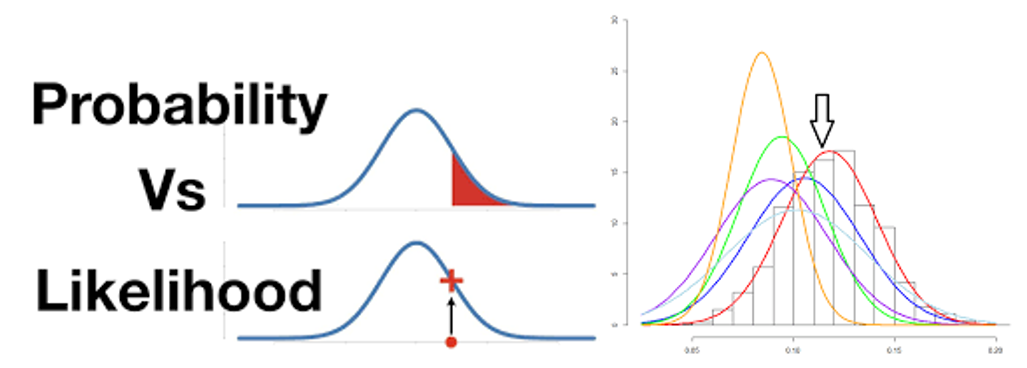
تفاوت تابع احتمال و تابع درستنمایی در نوع نگاه آنها به مسئله هست.
در تابع احتمال با ثابت نگه داشتن مقدار پارامتر، توزیع مقدار احتمال داده ها مورد بررسی قرار می گیرد. در صورتیکه در تابع درستنمایی با ثابت نگه داشتن مقادیر داده، مقدار احتمال درستی پارامتر بررسی می شود.
در برآورد ضرایب مدل رگرسیونی (h)، روش تخمین بیشینه درستنمایی (MLE) با در نظر گرفتن داده های ورودی X به مدل، به دنبال یافتن بهترین پارامترهای مدل (ضرایب بتا) است به طوری که بیشترین همخوانی را با داده های در نظر گرفته شده داشته باشد.
به علت کوچک بودن مقدار احتمال برای هر مقدار x معمولا از لگاریتم تابع درستنمایی در حل مسئله استفاده می شود و به همین دلیل تابع هدف این روش به عنوان Log – Likelihood نیز شناخته می شود.
ثابت می شود که در صورت برقراری فرض نرمال بودن توزیع خطا در مدل رگرسیون، برآورد حداقل مربعات یک برآورد MLE نیز محسوب می گردد.
روش کاهش گرادیان (Gradient Decent Method)
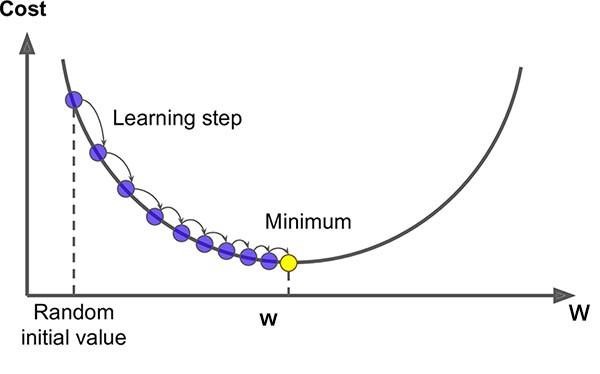
یکی دیگر از روش های برآورد ضرایب مدل رگرسیونی استفاده از روش کاهش گرادیان می باشد که با در نظر گرفتن مقدار تصادفی اولیه برای هر یک از ضرایب مدل و محاسبه میزان خطای پیش بینی در جهت کاهش خطا حرکت کرده و طی یک فرآیند تکراری به ضرایب بهینه همگرا می شود. این روش در مواقعی که با حجم داده های زیادی در تعداد مشاهدات و ویژگی ها مواجه باشیم (نیاز به حافظه زیادی برای محاسبات ماتریسی خواهد داشت) گزینه مطلوبی خواهد بود.
برآورد ضرایب مدل در الگوریتم شبکه عصبی عموما از روش کاهش گرادیان استفاده می نماید.
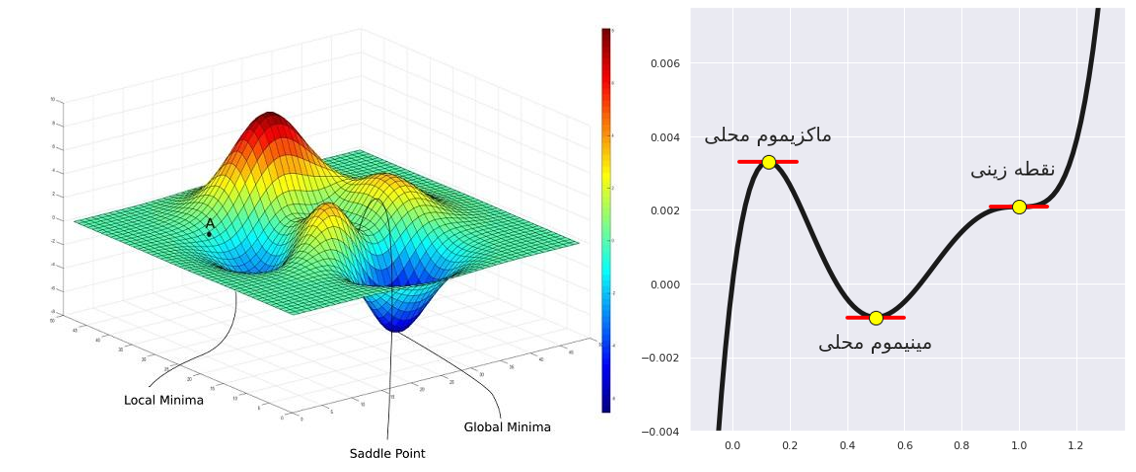
الگوریتم گرادیان کاهشی، یک الگوریتم بهینهسازی تکراری مرتبه-اول هست که مینیموم محلی در یک تابع مشتقپذیر را پیدا میکند. به عبارت دیگر گرادیان کاهشی الگوریتمی است که مینیمومهای محلی را در یک تابع پیدا میکند.
روش تنظیم سازی (Regularization Method)
برخی روش های توسعه یافته روی مدل رگرسیون حداقل مربعات، یافتن ضرایب مدل را به گونه ای انجام می دهند که علاوه بر کاهش خطای پیش بینی بطور همزمان کاهش پیچیدگی مدل را نیز لحاظ می نمایند. این روش ها که تحت عنوان روش تنظیم سازی شناخته می شوند، با اضافه کردن مجموع نرم اول یا دوم ضرایب به تابع بهینه سازی، عملیات برآورد ضرایب را انجام می دهند.
مقدار در این رابطه به عنوان پارامتر تنظیم می باشد و مقادیر بزرگتر آن منجر به سادگی بیشتر مدل می شود؛ به این معنی که تعداد ویژگی های با مقدار بتای معنادار کمتر شده و مدل ساده تری خواهیم داشت. در نتیجه تنظیم سازی روشی برای جلوگیری از بیش برازشی می باشد.
● رگرسیون لاسو (Lasso Regression)
در صورتیکه مقدار q = 1 باشد، به عنوان L1-Regularization شناخته شده و ویژگی مهم این روش در این می باشد که منجر به صفر شدن مقدار بتا برای تعداد قابل توجهی از ویژگی های کم اهمیت می شود. به همین دلیل مدل بدست آمده با این روش تحت عنوان مدل تنک (Sparse) روشی مناسب برای انتخاب ویژگی در داده های با ابعاد بالا شناخته می شود.
● رگرسیون ستیغی (Ridge Regression)
در صورتی که مقدار q = 2 باشد، به عنوان L2-Regularization شناخته شده و منجر به کوچک شدن میزان بتا برای ویژگی های کم اهمیت می شود (نزدیک به صفر) و بعلت فرم بسته توان دوم آن نسبت به حالت L1 پیچیدگی محاسباتی کمتری دارد.