خلاصه سازی آماری؛ کلیدِ فهم داده‌ها

ما در بخش «کاربرد آمار و احتمال در حوزه‌ی علم داده» یک دسته‌بندی داشتیم؛ گفتیم یک زیربنای تئوریک از احتمال وجود دارد که به کار می‌آید و روی آن، سه سطح ابزارهای آماری قرار می‌گیرند که به‌شدت پرکاربرد می‌شوند: یک‌سری ابزارها در حوزه‌ی خلاصه‌سازی داده‌ها، یک‌سری ابزارها در حوزه‌ی ارتباطی، و یک‌سری هم در حوزه‌ی مدل‌سازی.

در فرآیند EDA هم اشاره شد که بخش مدل‌سازی تقریباً کنار گذاشته می‌شود و تمرکز ما روی بخش «کانسپت احتمالی» و ابزارهای خلاصه‌سازی و ارتباط‌سنجی قرار می‌گیرد. تقریباً در بخش عملی هم ما با هر دو موضوع، به‌نوعی و به‌شکل پرکتیکال، خروجی گرفتیم و درباره‌شان صحبت کردیم.

اکنون می‌خواهیم وارد بخش مربوط به خلاصه‌سازی آماری بشویم. برخی از آن ابزارها و تکنیک‌هایی را که در پروژه‌ی اجرایی‌مان استفاده کردیم، این بار با دید بهتر و آکادمیک‌تر و کمی دسته‌بندی‌شده‌تر مطرح کنیم تا یک دید بهتر و جامع‌تر داشته باشیم.

ضرورت خلاصه‌سازی و مثال معدل

وقتی بحث خلاصه‌سازی آماری مطرح می‌شود، عموماً منظور مجموعه‌ای از شاخص‌هایی است که داده‌ها را «فشرده» می‌کنند. بگذارید مثالی بزنم: شما به‌عنوان یک دانشجو، کل فرآیند عملکرد آموزشی‌تان در چهار سال مقطع کارشناسی، در قالب یک عدد به‌عنوان معدل نمایش داده می‌شود؛ عملاً همه‌ی دروس، بر اساس ضریب و تعداد واحدشان، در یک عدد فشرده می‌شوند.

حال فرض کنید دانشجویی که معدلش ۱۵ است را با دانشجوی دیگری که معدل او هم حول‌وحوش ۱۵ است مقایسه کنیم. آیا می‌توان گفت عملکرد یکسانی دارند؟ در دنیای واقعی زیاد این اتفاق می‌افتد، اما متأسفانه این مقایسه دقیق نیست. چرا؟ چون ممکن است دانشجوی اول تمام دروسی که گذرانده تقریباً در بازه‌ی ۱۴ تا ۱۶ نمره گرفته باشد؛ یعنی ثبات عملکردی داشته و سطح توانمندی علمی‌اش مشخص بوده و نمراتش نزدیک به مرکز ثقل (همان معدل) قرار داشته‌اند. اما دانشجوی دوم ممکن است در برخی درس‌ها نمرات خیلی خوب ۱۹ و ۲۰ گرفته باشد و در برخی دیگر نمرات خیلی پایین، و در نهایت معدلش ۱۵ شده باشد.

همین مثال را به سطح کلاس ببرید: دو کلاس با معدل ۱۵. در یک کلاس، نمرات ممکن است همگن باشند؛ در کلاس دیگر بسیار پخش و پراکنده. این نشان می‌دهد وقتی می‌خواهیم «فشرده‌سازی» کنیم، نمی‌توانیم فقط با یک شاخصی مثل میانگین که مرکز ثقل را نشان می‌دهد، ماجرا را تمام‌شده بدانیم؛ این شاخص نمی‌تواند پاسخ‌گوی تمام اطلاعاتی باشد که در داده‌های خام وجود دارد. یک شاخص دیگر از جنس پراکندگی هم لازم است تا بگوید داده‌ها حول آن مرکز چگونه پخش شده‌اند.

دسته‌بندی شاخص‌ها: مرکزی و پراکندگی

به همین دلیل، در بحث خلاصه‌سازی می‌توانیم دسته‌بندی اصلی را این‌گونه داشته باشیم:

شاخص‌های مرکزی: مانند میانگین، مدین/میانه، و مد/نما (بیشترین فراوانی؛ در فارسی به «نما» هم گفته می‌شود).
شاخص‌های پراکندگی: مانند دامنه (Range)؛ یعنی از کمینه تا بیشینه چه بازه‌ای را پوشش می‌دهیم. انحراف معیار (Standard Deviation) و واریانس نیز از همین خانواده‌اند. همین‌طور دامنه‌ی بین چارکی (Interquartile Range/IQR).

این شاخص‌ها تمرکزشان بر اندازه‌گیری پراکندگی داده‌هاست. با توجه به مثال اول، نه شاخص‌های پراکندگی را می‌توان به‌تنهایی به کار برد و نه شاخص‌های مرکزی را؛ در هرجا که یک گروه از داده‌ها وجود دارد و قرار است توصیف یا مقایسه شود، باید این دو خانواده به‌صورت توأمان به کار گرفته شوند. این‌که در هر مسئله از کدام شاخص‌ها استفاده کنیم، بسته به مسئله، نیاز، و شناخت از ماهیت هر شاخص است.

شکل توزیع‌ها و اثر پراکندگی

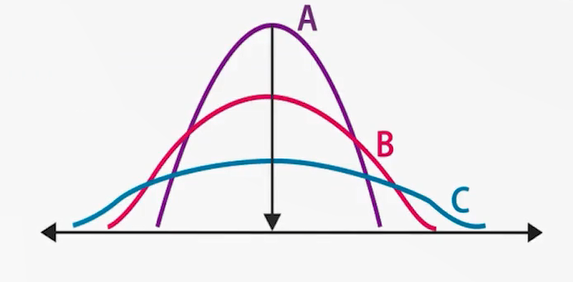
در تصویری که توضیح داده شد، سه توزیع مختلف از داده‌ها داریم (A، B، C) که همگی نرمال و متقارن‌اند. قله‌ی آن‌ها جایی است که میانگین (و در توزیع‌های متقارن، میانه و مد نیز) قرار دارند. یعنی نقطه‌ی مرکزی مشترک‌اند؛ اما شکل توزیع‌ها متفاوت است: در توزیع A پراکندگی کمتر و داده‌ها فشرده‌ترند، در حالی‌که در توزیع C پراکندگی بیشتر و داده‌ها گسترده‌ترند. همین تفاوت در شاخص‌های پراکندگی، شکل‌های مختلفی از یک توزیع نرمال را پدید می‌آورد و تفاوت‌های جدی در «پخش شدن» داده‌ها ایجاد می‌کند. پس باید همواره شاخص‌های مرکزی و پراکندگی کنار هم دیده شوند.

چولگی (Skewness) و حساسیت میانگین

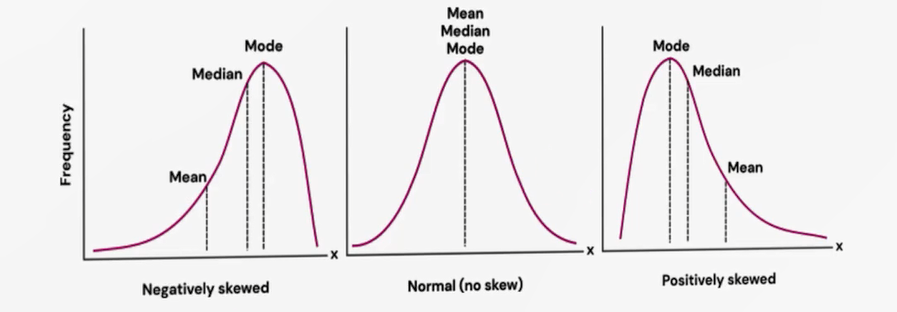
اگر توزیع نامتقارن باشد (چوله)، شرایط متفاوت است. وقتی «چوله به چپ» است، یعنی تعداد محدودی داده‌ی خیلی کوچک داریم و اکثریت داده‌ها در سطوح بالاتر متمرکزند. این داده‌های خیلی کوچک ــ با وجود تعداد اندک ــ میانگین را به سمت خودشان می‌کشند؛ میانگین به سمت چپ متمایل می‌شود، هرچند درصد داده‌های کمتر از میانگین کم باشد. این ویژگی میانگین است: نسبت به مقادیر افراطی (خیلی کوچک/خیلی بزرگ) حساس است و به سمت آن‌ها کشیده می‌شود.

در مقابل، میانه چون بر اساس مرتب‌سازی و موقعیت میانی تعریف می‌شود (۵۰٪ پایین‌تر و ۵۰٪ بالاتر)، تحت تأثیر مقدارهای خیلی کوچک یا خیلی بزرگ قرار نمی‌گیرد. مد نیز نقطه‌ی بیشترین فراوانی است و روی قله قرار می‌گیرد. اگر چوله به راست باشد، میانگین به سمت مقادیر خیلی بزرگ کشیده می‌شود.

این نکته در جاهای مهمی اثر دارد؛ مثلاً در الگوریتم‌های خوشه‌بندی (Clustering) که بر اساس «مرکز ثقل» داده‌ها خوشه می‌سازند، تفاوت میانگین و میانه می‌تواند نتایج مدل را تحت تأثیر قرار دهد. یا در برخورد با داده‌های پرت و جانشینی مقادیر گمشده: اگر بخواهیم یک مقدار گمشده را با یک عدد نماینده جایگزین کنیم، در داده‌های به‌شدت چوله، شاید میانه انتخاب بهتری از میانگین باشد.

البته باید توجه داشت محاسبه‌ی میانه به‌ویژه در حجم‌های بزرگ، هزینه‌ی محاسباتی بالایی دارد (نیازمند مرتب‌سازی کامل داده‌هاست). در حالی‌که میانگین صرفاً جمع و تقسیم است و سریع محاسبه می‌شود. همیشه یک تِریدآف وجود دارد: دقت/پایداری نتیجه‌ها در برابر هزینه‌ی اجرایی. تحلیل‌گر باید در هر مسئله انتخاب کند.

مثال سه مجموعه با میانگین برابر

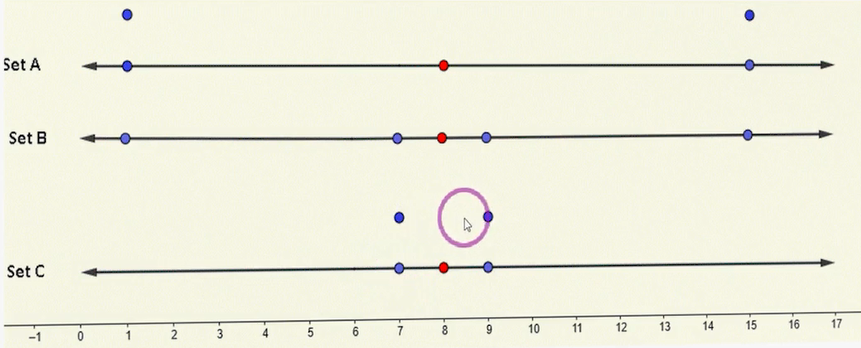
سه مجموعه‌ی A، B و C را در نظر بگیرید؛ هر کدام پنج رکورد دارند:

در A دو مقدار خیلی کوچک هم‌اندازه، دو مقدار خیلی بزرگ هم‌اندازه و یک مقدار وسط داریم. با توجه به فاصله‌ی برابر از دو طرف، میانگین دقیقاً در نقطه‌ی وسط (نشان‌گذاری‌شده با رنگ قرمز) قرار می‌گیرد.
در B چهار مقدار پراکنده داریم (یکی خیلی کوچک، یکی نسبتاً کوچک، یکی نسبتاً بزرگ، یکی خیلی بزرگ) و باز با فواصل برابر نسبت به نقطه‌ی پنجمِ وسط، میانگین در مرکز می‌ایستد.
در C چهار عدد خیلی نزدیک به مرکز ثقل‌اند (دو عدد نسبتاً کوچک و دو عدد نسبتاً بزرگ) و میانگین باز برابر با دو مجموعه‌ی دیگر است.

نتیجه: میانگین هر سه مجموعه برابر است، اما پراکندگی‌ها کاملاً متفاوت‌اند؛ A بیشترین پراکندگی، C کمترین، و B بینابین است. این تفاوتِ «پراکندگی با میانگین یکسان»، اهمیت شاخص‌های پراکندگی را نشان می‌دهد.

میانگینِ نمونه و جامعه

فرمول میانگین ساده است: مجموع مقادیر تقسیم بر تعداد. در نگارش آماری، میانگین نمونه را معمولاً با $Xˉ$ (ایکس‌بار) نمایش می‌دهند. میانگین جامعه معمولاً ناشناخته است و با $μ\mu$ نمایش داده می‌شود. چون ما معمولاً به کل جامعه دسترسی نداریم و با نمونه کار می‌کنیم، $Xˉ$ را به‌عنوان تخمینی از $μ\mu$ در نظر می‌گیریم.

واریانس و انحراف معیار: ایده و فرمول

برای سنجش پراکندگی، ایده‌ی انحراف معیار چنین است: ابتدا میانگین را به‌عنوان معیار می‌گیریم؛ سپس برای هر رکورد، «اختلاف با میانگین» را محاسبه می‌کنیم. اگر این اختلاف‌ها را مستقیم با هم جمع کنیم، به‌سبب مثبت و منفی بودن، جمع آن‌ها صفر می‌شود (میانگین مرکز ثقل است). برای رفع این مشکل، اختلاف‌ها را به توان دو می‌رسانیم و سپس از آن‌ها میانگین می‌گیریم؛ حاصل، واریانس است. برای بازگرداندن مقیاس به واحد اصلی داده‌ها، جذر واریانس را می‌گیریم؛ این می‌شود انحراف معیار.

مثلاً اگر انحراف معیار ۲ باشد و میانگین ۸، یعنی داده‌ها به‌طور متوسط حدود دو واحد از میانگین فاصله دارند. واحدِ انحراف معیار با واحدِ داده‌های اصلی هم‌مقیاس است؛ اما واریانس به‌دلیل مجذور بودن، به‌راحتی قابل قیاس با مقادیر اصلی نیست؛ به همین دلیل معمولاً از انحراف معیار استفاده می‌شود.

در مثال سه‌گانه‌ی A/B/C، اگر انحراف معیار را حساب کنیم: C کمترین، A بیشترین و B حدوسط است.

وقتی اندازه‌ی نمونه‌ها متفاوت است: خطای استاندارد میانگین

وقتی می‌خواهیم دو یا چند گروه را مقایسه کنیم و اندازه‌ی نمونه‌ها برابر نیست، برای خنثی کردن اثر اندازه‌ی نمونه و مقایسه‌ی منصفانه، از خطای استاندارد میانگین (Standard Error of the Mean) استفاده می‌کنیم:

هرجا انحراف معیار را دارید، کافی است آن را بر جذر تعداد نمونه تقسیم کنید تا $SESE$ به دست آید. آنگاه می‌توانید SE گروه‌ها را با هم مقایسه کنید (نه صرفاً SD را)، تا بگویید کدام گروه پراکندگی بیشتری (نسبت به اندازه‌ی نمونه‌اش) دارد.

فاصله‌ی اطمینان (Confidence Interval)

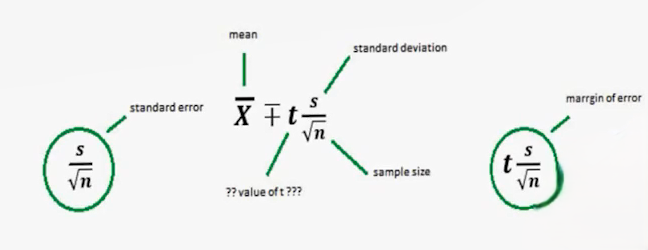
در آمار، ترکیب شاخص مرکزی و پراکندگی به برآورد فاصله‌ای می‌انجامد: فاصله‌ی اطمینان. فرمول رایج برای میانگین:

یعنی از میانگین، مقداری برابر با $t$ ضرب‌در خطای استاندارد کم و زیاد می‌کنیم؛ بازه‌ای پیرامون مرکز ثقل ایجاد می‌شود (حد پایین و حد بالا). می‌توان این‌طور گفت: هر گروه را با «مرکز» و یک «سایه‌ی اطرافش» نمایش می‌دهیم؛ آن سایه همان CI است.

اگر دو گروه داشته باشیم:

همپوشانی CIها ⇒ از نظر آماری دلیلی برای تفاوت نداریم (برابر در نظر گرفته می‌شوند).
بدون همپوشانی ⇒ تفاوتِ معنادار آماری دارند.

این ایده اساس بسیاری از آزمون‌های فرض نیز هست.

نقش توزیع t و تقریب ذهنی ۹۵٪

ضریب $tt$ بر پایه‌ی توزیع t به‌دست می‌آید. توزیع t یک توزیع متقارن، زنگوله‌ای‌شکل و بسیار نزدیک به نرمال است؛ در واقع، نرمال استاندارد حالت خاصی از t است که وقتی درجه‌ی آزادی به بی‌نهایت میل کند به آن نزدیک می‌شود. t کمی «جمع‌وجورتر» از نرمال است (پهنای کمتر در مرکز) و دم‌های ضخیم‌تری دارد.

برای فاصله‌ی اطمینان ۹۵٪ (سطح خطای ۵٪)، معمولاً به‌طور ذهنی می‌توان گفت: «تقریباً دو برابر $SESE$ را از میانگین کم و زیاد کنید.» البته مقدار دقیق $t$ به درجه‌ی آزادی وابسته است و کمی کمتر از ۲ می‌شود، اما این قاعده‌ی دو برابر، یک تقریب ذهنی سریع می‌دهد.

مثال ذهنی در پروژه‌ی عملی

فرض کنید در خروجی پروژه‌ی عملی، برای «سن» یا «سدیم» یا «پتاسیم»، میانگین و انحراف معیار گزارش شده است. با تقسیم SD بر $n\sqrt{n}$ به $SESE$ می‌رسیم؛ دو برابرش را از میانگین کم‌وزیاد می‌کنیم و تقریباً CI 95% را داریم.

تعبیر درست «۹۵٪»: تکرارپذیری نمونه‌گیری

چرا ۹۵٪؟ چون ما با نمونه کار می‌کنیم. اگر از یک جامعه، بارها نمونه بگیریم، $Xˉ$ تغییر می‌کند (حتی $n$ هم ممکن است تغییر کند). اگر این «بازی نمونه‌گیری» ۱۰۰ بار تکرار شود، در حدود ۹۵ بار، میانگینِ جامعه داخل CI محاسبه‌شده قرار می‌گیرد و ۵ بار خارج می‌ماند.

پس اگر یک‌بار، در یک نمونه، دقت مدل مثلاً ۹۴٪ شد، این الزاماً واقعیتِ جامعه نیست؛ شاید همان یکی از همان «۵ موردِ استثنا» باشد. اگر پنج یا ده بار دیگر تکرار کنیم، ببینیم اغلب دفعات نتایج در ۷۰–۸۰٪ می‌نشینند و فقط یک‌بار ۹۴٪ شده است. بنابراین، برای اطمینان بیشتر باید نمونه‌گیری و فرآیند را چندبار تکرار کنیم تا ببینیم «مرکز ثقل» میانگین‌ها کجاست و اکثریت در چه بازه‌ای قرار می‌گیرند؛ تا تصمیمات و ارائه‌ی نهایی‌مان (برای کارفرما) تحت‌تأثیر یک خطای احتمالی ناشی از همان ۵٪ پذیرفته‌شده قرار نگیرد.

منطق مقایسه در آمار (میانگین تنها کافی نیست)

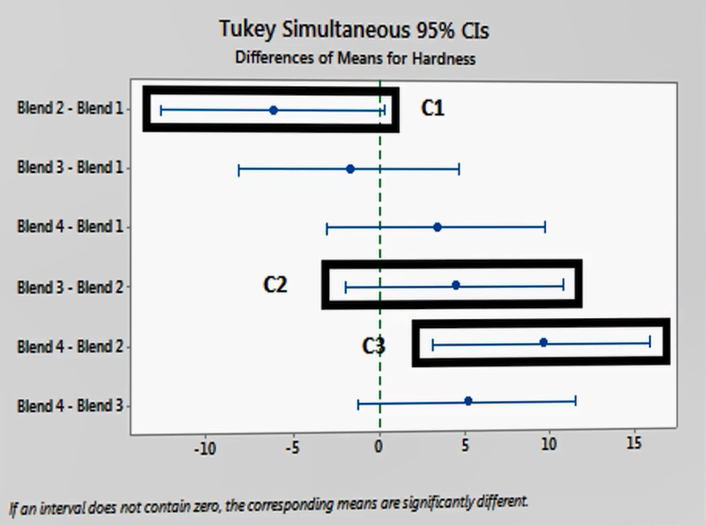
در ریاضیات، اگر $x=yx=y$ و $y=zy=z$ ، نتیجه می‌گیریم $x=zx=z$ . اما در آمار، منطق متفاوت است. فرض کنید سه گروه داریم با مراکز و CI مشخص. اگر فقط به مراکز نگاه کنیم، شاید «C2» بهتر از «C1» به‌نظر برسد. اما وقتی CIها را می‌بینیم و همپوشانی آن‌ها را بررسی می‌کنیم، ممکن است نتیجه شود C1 و C2 از نظر آماری برابرند. همین‌طور C2 و C3 نیز. ولی اگر بین C1 و C3 هیچ اشتراکی نباشد، می‌گوییم تفاوت معنادار دارند.

این مثال نشان می‌دهد اگر فقط بر اساس اعدادِ شاخص‌های مرکزی تصمیم بگیریم، ممکن است به بیراهه برویم. در آمار، هر جا گروه‌ها مقایسه می‌شوند، باید عددِ مرکز و سایه‌ی اطرافش (شاخصی از پراکندگی) همزمان دیده شوند؛ در قالب CI.

همپوشانی ⇒ عدم تفاوت معنادار، عدم همپوشانی ⇒ تفاوت معنادار (که بعدها می‌بینیم معادل آزمون t است).

خلاصه‌سازی بصری (Chartها)

در کنار خلاصه‌سازی عددی، خلاصه‌سازی بصری هم بسیار مهم است و سریع یک حس از وضعیت داده می‌دهد:

برای داده‌های کیفی:
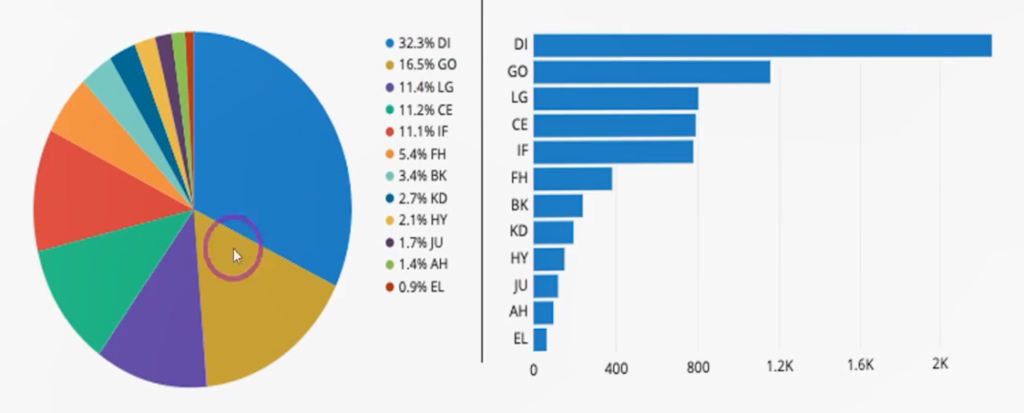
- Pie Chart (دایره‌ای): سهم هر گروه از کل را نشان می‌دهد؛ اگر گروه‌ها زیاد شوند، خوانایی پایین می‌آید.
- Bar Chart (میله‌ای): می‌تواند مرتب‌شده یا نامرتب نمایش داده شود؛ برای داده‌های کیفی بسیار مناسب است.

برای داده‌های کمی/پیوسته:
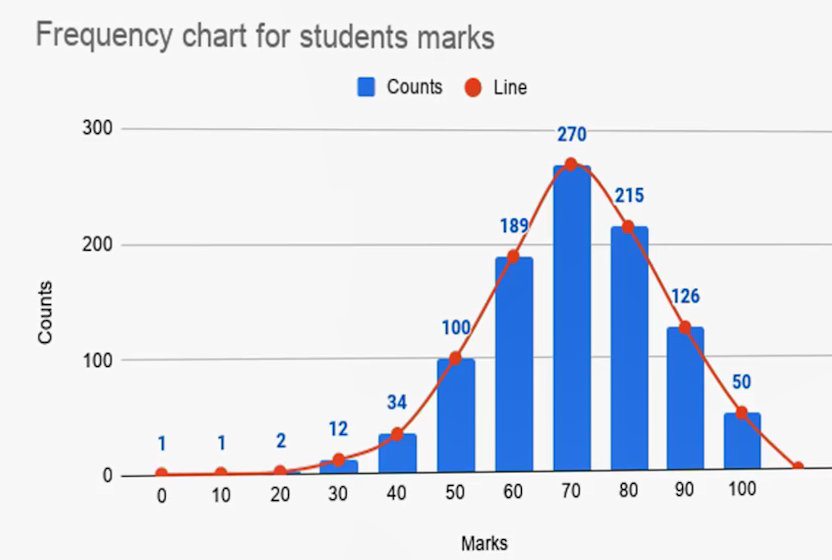
- Histogram: مقدار پیوسته را «بین‌بندی» (Binning) می‌کند (مثلاً ۰ تا ۱۰۰ را به بازه‌های ۱۰تایی/۵تایی). هرچه تعداد بین‌ها بیشتر باشد، حس پیوستگی بهتر دیده می‌شود. معمولاً ۲۵ تا ۳۰ بین پیشنهاد می‌شود. (هیستوگرام از نظر کارکرد شبیه بارچارت است، اما برای داده‌های کمی و با رعایت همسایگی طبقات.)

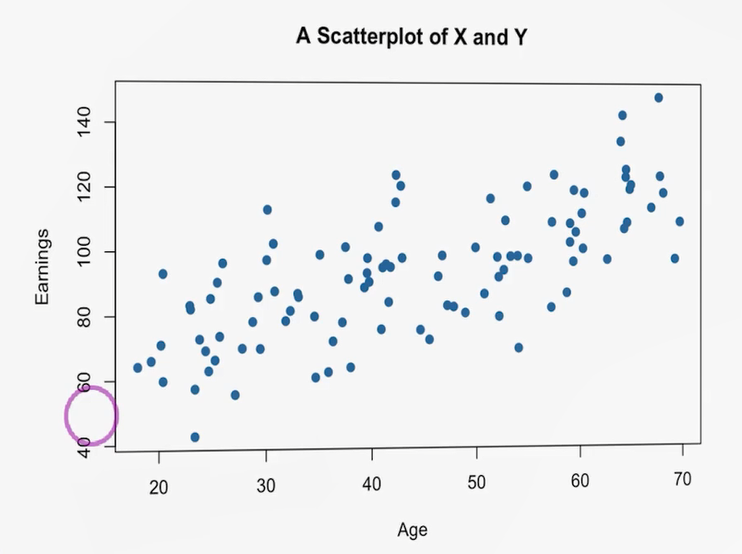
Scatter Plot (پراکنش): برای دیدن روابط (خطی/غیرخطی) بین دو متغیر بسیار پرکاربرد است. همان‌طور که در پروژه برای سدیم و پتاسیم استفاده شد؛ یا مثلاً محور افقی سن و محور عمودی درآمد: با افزایش سن، روند درآمد افزایشی دیده می‌شود و خطی از مرکز ثقل نقاط با شیب مثبت قابل ترسیم است.

نمودار سری‌زمانی (Time Series): هرجا داده‌ها ترتیبی/زمانی باشند (مثل نمودارهای مالی)، برای دیدن قله‌ها، افت‌ها و الگوهای نوسانی بسیار مفید است.

کیفیت داده‌ها (Data Quality)

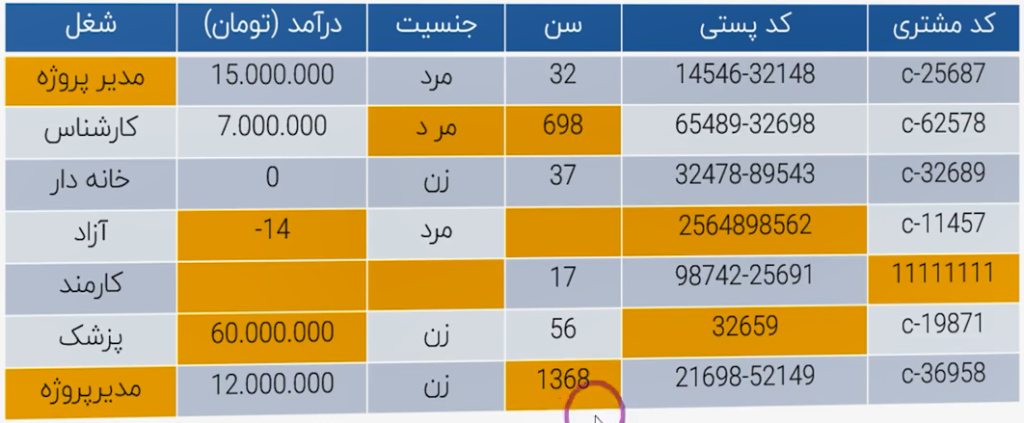
آخرین موردی که در بحث خلاصه‌سازی آماری ــ به‌ویژه در فاز Data Understanding و بخش کیفیت داده ــ شناسایی و ارزیابی می‌شود، Data Quality است. چندین نوع «سوءکیفیت» ممکن است در داده‌ها رخ دهد. در مثال ارائه‌شده، سعی شده همه‌ی خطاهای عمومی که ممکن است در داده‌ها وجود داشته باشد نشان داده شود:

ورود دستی/منوال و تفاوت نگارشی: مثلاً در ستون «مدیر پروژه»، یک‌جا «مدیر‌پروژه» چسبیده است و جای دیگر «مدیر پروژه» با فاصله. برای کامپیوتر این‌ها دو مقدار متفاوت‌اند (دو آبجکت/دو کلاس جدا). چنین خطاهایی در ورود دستی داده‌ها بسیار رایج است و می‌تواند توزیع کلاس‌ها را عوض کند (به‌جای یک کلاس «مدیر پروژه»، دو مقدار جدا با فراوانی‌های کوچک‌تر خواهیم داشت).
مقادیر غیرمنطقی: در ستون «درآمد» عدد «ـ۱۴» ثبت شده است؛ درآمد منفی منطقی نیست. یا درصد بالاتر از ۱۰۰٪ ثبت شده است. ممکن است خطا سیستمی یا انسانی باشد.
مقادیر گمشده (Missing Values): سلول‌های خالی که اگر با آن‌ها برخورد نشود، خیلی وقت‌ها مدل خودکار آن رکورد را نادیده می‌گیرد. نباید به‌خاطر یک سلول خالی، یک ردیف کاملِ مفید را از دست بدهیم؛ باید در مرحله‌ی Data Understanding آن‌ها را پیدا و برای‌شان استراتژی تعیین کنیم.
نقاط پرت (Outliers): مثلاً در «درآمد»، مقادیر ۱۵، ۷، ۱۲ میلیون داریم و ناگهان «۶۰ میلیون». این مقدار پرت، توزیع را به‌شدت چوله می‌کند و بسیاری از الگوریتم‌ها (که بر فرض‌های توزیعی تکیه دارند) را دچار مشکل می‌کند. باید Outlierها شناسایی و با استراتژی مناسب تعدیل/اصلاح شوند تا مدل‌سازی تحت‌الشعاع قرار نگیرد.

ناسازگاری‌ها: در ستون «جنسیت»، یک‌جا «مرد» صحیح ثبت شده، جای دیگر «مر د» (با فاصله‌ی داخل کلمه). در ستون «سن» مقدار ۶۹۸ ثبت شده که آشکارا اشتباه است؛ «۱۳۶۸» احتمالاً سال تولد بوده و قابل اصلاح است، اما «۶۹۸» نامعتبر است. در «کد پستی»، فرمت‌ها یکسان نیستند (با/بی‌خط تیره). در «کد مشتری»، مقداری مانند «۱۱» که احتمالاً کد تستی پایگاه داده بوده، کنار کدهای واقعی آمده است. همه‌ی این‌ها باید شناسایی و یکدست شوند.

جمع‌بندی دسته‌بندی خطاهای کیفیت

خارج از بازه‌ی منطقی (Out of Range)
ناسازگار (Inconsistent Data)
پرت (Outliers): هم در سطح نقطه (Point Outlier) و هم در سطح رکورد (Record Outlier). رکورد پرت معمولاً با تحلیل‌های چندمتغیره و روش‌هایی مثل خوشه‌بندی شناسایی می‌شود.
مقادیر گمشده (Missing Data)

برخورد با مقادیر گمشده

دو رویکرد اصلی داریم:

حذف (Deletion): حذف رکورد دارای مقدار گمشده.
جانشینی (Imputation): جایگزینی مقدار تخمینی (با میانگین، میانه/مدین، مد/نما، روش‌های درون‌یابی یا مدل‌های پیچیده‌تر). هرچه روش پیچیده‌تر، دقت بالاتر اما هزینه‌ی محاسباتی بیشتر.

با توجه به آن‌چه پیش‌تر دیدیم، در داده‌های چوله، استفاده از میانه برای جانشینی معمولاً بهتر از میانگین است؛ چون میانگین شدیداً تحت‌تأثیر پرت‌ها قرار می‌گیرد.