- مقاله‌ی حاضر دایکه ادامه‌ی همان مثال مطالعه‌ی موردی است که طی چند هفته‌ی گذشته کار می‌کردیم. چهار بخش قبلی را می‌توانید در لینک‌های زیر بیابید:
در این مقاله، راجع به نوعی درخت تصمیم به‌نام درخت رگرسیون و دسته‌بندی ([CART[1) به‌منظور توسعه‌ی مدل سریع و نخراشیده‌ای برای همان مثال مطالعه‌ی موردی قبلی بحث می‌کنیم. اما پیش از شروع بحث، اجازه دهید اصول موارد زیر را بررسی کنیم:
درخت تصمیم
بیاید بپذیریم که همه‌ی ما پیش از برداشتن تکه‌ای پیتزا از داخل جعبه، سریعاً اندازه‌ی تکه و نسبت‌‌های مواد روی آن را تحلیل می‌کنیم. در این بهینه‌سازی، عمدتاً در جستجوی بزرگترین تکه‌ی حاوی بیشترین مواد موردعلاقه‌تان هستید (و احتمالاً از تکه‌هایی که حاوی موادی هستند که اصلاً دوست ندارید پرهیز می‌کنید). با این اوصاف، ترجیحاً این پسربچه (در شکل) را حریص نمی‌نامیم. او صرفاً می‌کوشد کیک تولدش را طوری ببرد که تکه‌ی مدنظرش حاوی بیشترین مقدار از طعم موردعلاقه‌اش باشد.
گوشه‌ی بالایی کیک پسند ذائقه‌ی اوست؛ حاوی گیلاس‌های قرمز محبوبش و مقدار نه چندان زیادی از سیب سبز. او باید فقط با دو ضربه چاقو برش تمیزی ایجاد کند، وگرنه مهمانان جشن‌اش از کاربرد ناشیانه‌ی او از چاقو لذت نخواهند برد. این پسربچه می‌تواند با به‌کارگیری مهارتی بی‌نقص و استفاده از درخت تصمیم در مغزش، تکه‌ی کاملی ببرد تا از طعم آن لذت وافی را ببرد. اجازه دهید به هنرورزی این پسربچه نگاهی بیندازیم:
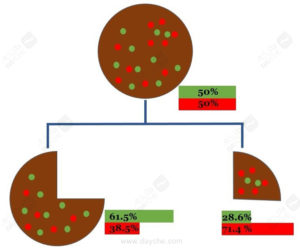
کیک درخت تصمیم – الگوریتم CART
او برش کیک را با نسبت‌هایی از تکه‌های قرمز و سبز (۵۰٪ – ۵۰٪) آغاز کرد. یادتان باشد که او بیشترین تعداد از تکه‌های قرمز و کمترین تعداد از تکه‌های سبز را روی برشش می‌خواست. برش او، یعنی یک‌چهارم کیک، ۷۱ درصد تکه‌ی قرمز و ۲۹ درصد تکه‌ی سبز دارد. بد هم نیست! الگوریتم درخت تصمیم دقیقاً این‌طوری کار میکند. درست مثل مسئله‌ی بالا، الگوریتم CART می‌کوشد گره ریشه (کل کیک) را فقط به دو تکه (نه بیشتر) برش دهد/ تقسیم کند. هرچند، الگوریتم‌های درخت تصمیم دیگری هم هستند که در مقاله‌ی بعدی مطرح می‌کنیم؛ این الگوریتم‌ها قادرند گره ریشه را به قطعات زیادی تقسیم کنند. باید خاطرنشان کنم که گرچه در این مقاله، از داده‌های مجزا (مثل گیلاس‌های قرمز و سیب‌های سبز) برای درخت تصمیم استفاده می‌کنیم، اما CART قادر است داده‌های کمی مثل سن، فاصله و غیره را هم به‌طور مساوی تقسیم کند. بیایید الگوریتم درخت تصمیم CART را بیشتر بررسی کنیم.درخت رگرسیون و دسته‌بندی (CART)
از نظر من، الگوریتم‌هایی مثل الگوریتم پیج رنک گوگل[2]، الگوریتم‌های رمزنگاری اَلن تورینگ یا چندتایی از الگوریتم‌هایی یادگیری ماشین خیلی شگفت‌انگیزند. برای من، الگوریتم‌ها بازتابی از اندیشه‌ی ساختاریافته‌ی ابرازشده ازطریق منطق هستند. برای مثال، الگوریتم CART توسیعی از فرایندی‌ست که داخل مغز این پسربچه، ضمن تقسیم‌کردن کیک تولدش رخ می‌دهد. او سعی داشت بزرگترین تکه‌ی حاوی بیشترین گیلاس و کمترین سیب را برای خودش ببرد. در این مسئله، او دو هدف داشت. ۱. جداسازی بزرگترین تکه با برشی تمیز ۲. بیشینه‌سازی تعداد گیلاس‌های روی این تکه، ضمن کمینه‌سازی تعداد سیب‌های سبز الگوریتم درخت تصمیم CART تلاشی برای دستیابی به دو هدف فوق است. معادله‌ی زیر نمایشی از ترکیب این دو هدف است. از این معادله نترسید، این معادله درواقع خیلی ساده است؛ پس از حل مثالی در قسمت بعدی، متوجه سادگی این معادله خواهید شد.
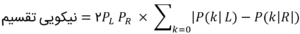
• اولین جمله‌ی معادله‌ی فوق، یعنی 
هدف اول را کنترل میکند تا بزرگترین تکه بریده شود. اجازه دهید این جمله را «(تکه‌ی بزرگ)Ψ» بنامم، چرا که مرا یاد هدف ماورای این معادله‌ی ریاضی می‌اندازد.
• این در حالی‌ست که جمله‌ی دوم، یعنی 
هدف دوم را کنترل میکند. این جمله را «(انتخاب گیلاس‌ها)Ψ» می‌نامم.
برای مثال، ۱، ۰ = k است؛ در معادله‌ی فوق، سیب‌های سبز = ۰ و گیلاس‌های قرمز = ۱ هستند. یادتان باشد که برای مطالعه‌ی موردی ما با کمپین‌های بازاریابی، ۰، ۱ = k، مشتریان با واکنش مثبت ([r[3) و بدون واکنش مثبت ([nr[4) می‌شود. همین‌طور، برای مقالات امتیازبندی اعتبار و مطالعه‌ی موردی بانکداری (در آینده به بخش مقالات دایکه اضافه می شود)، ۰، ۱ = k، نکول‌کننده و نکول‌نکننده[5] می‌شود. هرچند، فلسفه‌ی درخت تصمیم و CART برای همه‌ی این مثال‌ها و مسائل دسته‌بندی عَملی‌تر همچنان یکی است. اجازه دهید پیش از تشریح اجزاء معادله‌ی نیکویی تقسیم فوق، برخی از مهمترین اصطلاحات فنی الگوریتم درخت تصمیم CART را تعریف کنم.
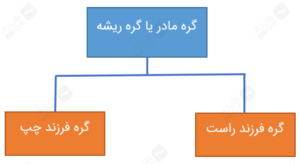
اصطلاحات فنی درخت تصمیم CART
تعاریف اجزاء معادله‌ی نیکویی تقسیم در زیر ارائه شده‌اند: L: گره فرزند چپِ گره ریشه R: گره فرزند راستِ گره ریشه
مطالعه‌ی موردی خرده‌فروشی – درخت تصمیم (CART)
به مثال مطالعه‌ی موردی خرده‌فروشی برمی‌گردیم؛ در این مثال، شما مدیر ارشد تحلیل و رئیس راهبرد کسب‌وکار فروشگاه آنلاینی به‌نام شرکت درس‌اسمارت هستید که در حیطه‌ی پوشاک تخصص دارد. در این مثال موردی، قصد دارید عملکرد کمپین‌های آتی را بهبود بخشید. برای دستیابی به این هدف، داده‌های برگرفته از کمپین قبلی، که کاتالوگ‌های کالاها را مستقیماً به صدها هزار مشتری از پایگاه مشتریان کاملِ چند میلیون نفری ارسال کرد، را تحلیل می‌کنید. نرخ دریافت واکنش مثبت کل برای این کمپین، ۴.۲ درصد بود. شما کل صدها هزار مشتری متقاضی را برمبنای فعالیت ۳ ماه قبلی‌شان پیش از شروع کمپین، به سه دسته تقسیم کردید. جدول زیر، توزیع مشابهی را ارائه میکند. در این جدول، نرخ موفقیت، درصد مشتریانِ با واکنش مثبت (r) به کمپین از بین کل مشتریان متقاضی است.
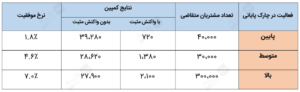
همان‌طور که می‌دانید، الگوریتم درخت تصمیم CART گره ریشه را فقط به دو گره فرزند تقسیم میکند. بنابراین، برای این داده‌ها، CART می‌تواند سه ترکیب از درخت‌های دوتایی بسازد (جدول زیر). باید بفهمیم بهترین تقسیم بین این سه ترکیب کدام است. نتایج در جدول زیر ارائه شده‌اند.
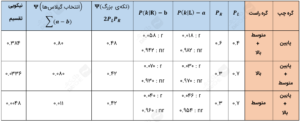
اجازه دهید در محاسبه‌ی هر یک از ستون‌های درخت بالا کمک‌تان کنم. برای انجام محاسبات زیر، از اولین ردیف (یعنی گره چپ: گره پایین و بالا: متوسط + بالا) استفاده می‌کنیم و پس از آن، می‌توانید مابقی محاسبات را خودتان انجام دهید. برای شروع، 
را به‌روش زیر محاسبه می‌کنیم:
حالا محاسبه‌ی (تکه‌ی بزرگ)Ψ به سادگی زیر می‌شود:
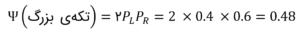
حالا به بخش بعدی معادله، یعنی (انتخاب گیلاس‌ها)Ψ می‌پردازیم. حواستان باشد که r معرف مشتریان با واکنش مثبت و nr معرف مشتریان بدون واکنش مثبت به مثال کمپین‌مان است.
ممکن است بخواهید دو جمله‌ی دیگر یعنی 
را هم پیش از جایگزاری آنها در معادله‌ی زیر، برای دستیابی به مقدار (انتخاب گیلاس‌ها)Ψ محاسبه کنید.
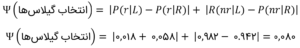
با این حساب، محاسبه‌ی پایانی ستون آخر، یعنی نیکویی تقسیم می‌ماند که به‌صورت زیر انجام می‌شود:
کار نهایی، یافتن بیشترین مقدار نیکویی تقسیم در ستون انتهایی است. این محاسبه، درخت تصمیم زیر را ازطریق الگوریتم CART، با پایین روی گره چپ و متوسط + بالا روی گره راست، تولید میکند.
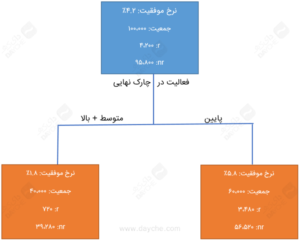
درخت تصمیم – نتیجه‌ی نهایی الگوریتم CART
این بینش کسب‌وکار مهمی است؛ به‌علاوه این‌که افراد با فعالیت بالاتر، واکنش بهتری به کمپین‌ها نشان می‌دهند. موافقم که این امر از جدول اول در بالا نیز واضح بود، اما ما علم خلق درخت تصمیم با استفاده از الگوریتم CART در فرایند را یاد گرفته‌ایم. زمانی‌که با مجموعه‌داده‌ی بزرگی سروکار دارید و می‌خواهید درخت تصمیمی ازطریق جزءبندی بازگشتی بسازید، این مهارت خیلی مفید خواهد بود.و اما حرف آخر
بسیار خُب، دفعه‌ی بعدی که آن تکه پیتزا را انتخاب می‌کنید، درخت تصمیم تکاملی را به یاد آورید که در بیشینه‌سازی شانس انتخاب بهترین تکه به شما کمک میکند. هر از گاهی، شاید بخواهید آن بهترین تکه را برای کَس دیگری کنار بگذارید – شرط می‌بندم به همان اندازه حس خوشایندی خواهید داشت! در مقاله‌ی بعدی دایکه، این مفهوم درخت تصمیم دارایِ گره فرزند دوتایی ازطریق الگوریتم CART را با استفاده از سایر الگوریتم‌ها، به درخت تصمیمی با بیش از دو گره بسط می‌دهیم. تا بعد![1] classification and regression tree [2] Google’s PageRank algorithm [3] responded [4] not-responded [5] loan defaulters & non-defaulters
