در یادگیری مدل شبکه عصبی با تعریف تابع هزینه (زیان) مشابه مدل های رگرسیونی، به دنبال تعیین مقادیر وزن بهینه می باشیم به طوری که تابع هزینه را مینیمم کند.
تفاوت مهم در شبکه عصبی MLP اینست که به علت وجود پرسپترون های متعدد (مدل های مینیاتوری کوچک) تغییرات جزئی در مقدار هر وزن، در مقادیر سایر پرسپترون ها نیز اثرگذار است و بهینه سازی تابع هزینه را پیچیده تر می کند.
بهینه سازی تابع هزینه و برآورد وزن ها در این مدل بر اساس روش کاهش گرادیان (Gradient Decent) انجام می شود و جهت بروزرسانی وزن ها در لایه ها نیز از رویکرد پس انتشار (Backpropagation) استفاده می شود.
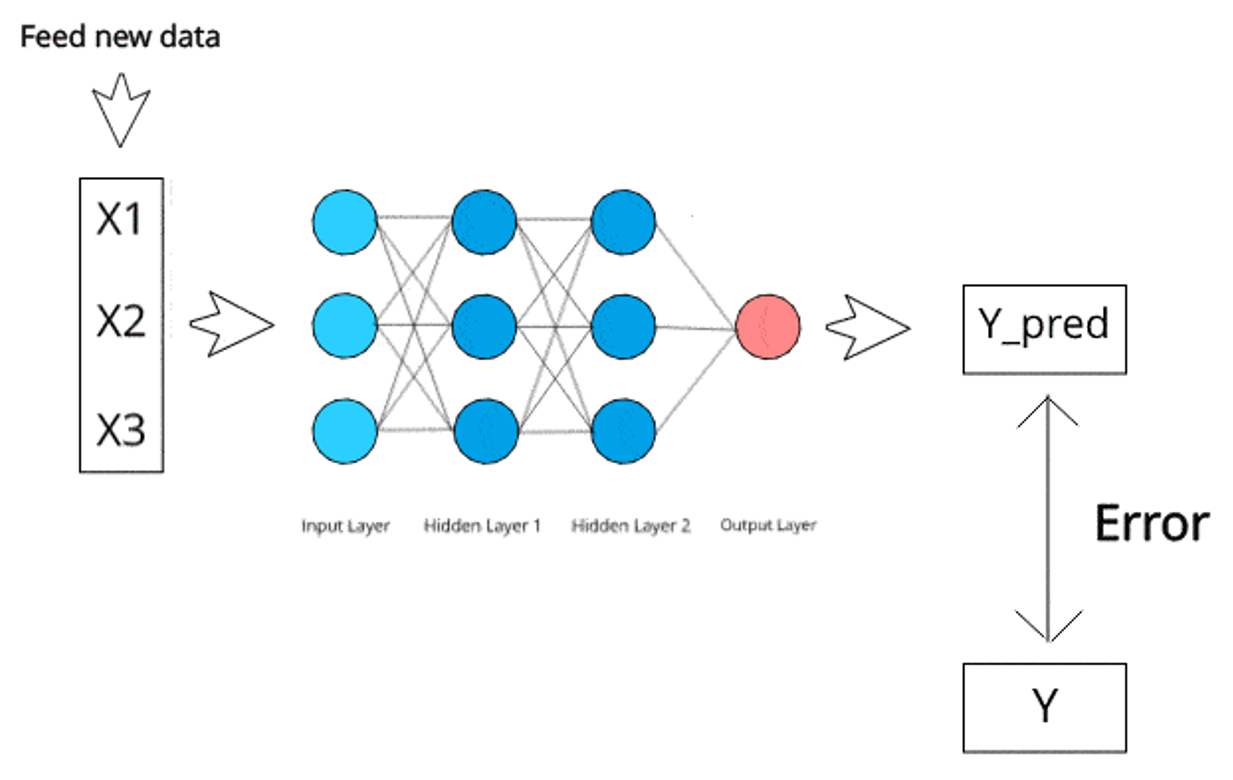
تابع هزینه (زیان) در شبکه عصبی
در مسئله رگرسیون، مشابه الگوریتم رگرسیون خطی از میانگین مجذور خطای مدل (MSE) استفاده می شود.
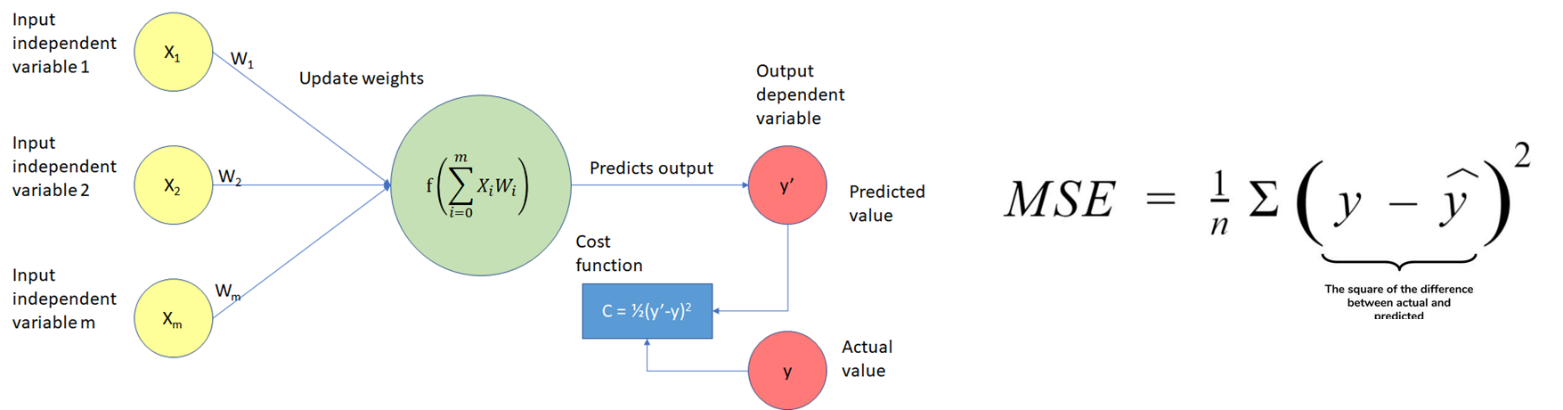
در مسئله رده بندی، مشابه الگوریتم رگرسیون لجستیک از تابع کراس آنتروپی (Cross Entropy) استفاده می شود.

روش کاهش گرادیان (Gradient Decent Method)
این روش با در نظر گرفتن مقدار تصادفی اولیه برای هر یک از ضرایب مدل (وزن ها) و محاسبه میزان خطای پیش بینی در جهت کاهش خطا حرکت کرده و طی یک فرآیند تکراری به ضرایب بهینه همگرا می شود. در واقع با تعیین گرادیان تابع هزینه که شامل برداری از مشتقات جزئی به تفکیک هر ضریب (وزن ها) است و حرکت در جهت بیشترین شیب، در یک فرآیند تکراری و گام به گام به سمت مینیمم تابع حرکت می کند.

هر عنصر بردار گرادیان به ما نشان می دهد تغییر جزئی در هریک از مقادیر وزن ها به چه میزانی در جهت کاهش گرادیان تاثیر دارد. بنابراین می توان تعیین کرد کدام وزن و به چه مقداری تغییر نماید.

روش پس انتشار (Backpropagation Method)
برخلاف جهت حرکت رو به جلوی شبکه عصبی MLP که مقادیر ورودی را لایه به لایه به سمت نورون های خروجی منتقل می کند، روش پس انتشار مقدار خطای محاسبه شده در نرون آخر را لایه به لایه به نورون های لایه ورودی منتقل می کند.

الگوریتم یادگیری شبکه عصبی و اثر نرخ یادگیری

مثال: محاسبه روش پس انتشار در یک پرسپترون


تنظیم پارامترهای مدل شبکه عصبی
تعداد لایه پنهان: هیچ قانون و رابطه ای برای تعیین تعداد لایه های مناسب شبکه عصبی وجود ندارد؛ ولی می توان ثابت کرد اغلب مسائل غیر خطی در رگرسیون و رده بندی با یک لایه پنهان قابلیت مدلسازی دارند و همچنین با دو لایه پنهان می توان هر شکل و فرمی از روابط غیر خطی را مدل کرد.
تعداد نرون های پنهان: تعیین دقیق تعداد نرون ها در لایه های پنهان نیز، هیچ راهکار محاسباتی ندارد و برای هر مسئله بایستی بر اساس آزمون و خطا و ارزیابی نتایج مدل با تنظیم پارامترهای مختلف بدست آید.
در برخی از منابع، قواعدی برای تنظیم اولیه شبکه عصبی معرفی شده و بر اساس ارزیابی نتایج اولیه، می توان به کم یا اضافه کردن نرون ها و لایه های شبکه عصبی پرداخت:
- تعداد نرون های لایه پنهان بایستی در بازه تعداد نرون های خروجی و ورودی باشد.
- تعداد نرون های لایه پنهان میانگین تعداد نرون های لایه ورودی و خروجی باشد.
- تعداد نرون ها در لایه های پنهان طوری تعیین گردد که ساختار هرمی شکل شبکه عصبی از ورودی به خروجی حفظ شود.
دوره (Epoch): در یادگیری مدل های شبکه عصبی، مجموعه داده های آموزشی بیش از یک بار در فرآیند یادگیری وارد شده و در تعیین وزن های مدل نقش بازی می کنند. به هر بار تکرار مجموعه داده یک چرخه یا دوره (Cycle or Epoch) گفته می شود افزایش این مقدار باعث می شود، هر رکورد در مجموعه داده های آموزشی، بارها در فرآیند یادگیری مدل وارد شده و منجر به بهبود نتایج مدل شود.
اندازه بسته (Batch Size): در یادگیری مدل های شبکه عصبی، می توان با تقسیم مجموعه داده های آموزشی به تعداد برابر از بسته هایی در اندازه حداقل یک رکورد تا حداکثر به تعداد کل داده های آموزشی، فرآیند بروزرسانی وزن های مدل در روش کاهش گرادیان را انجام داد. به این معنی که پس از اندازه گیری خطای پیش بینی در هر بسته از داده های آموزشی، محاسبات کاهش گرادیان انجام شده و وزنهای مدل با روش پس انتشار اصلاح می شوند.
مثال: فرض کنید 100 رکورد آموزشی داریم و تنظیمات مدل شبکه عصبی با اندازه بسته 5 و تعداد 1000 دوره انجام شده است. بنابراین در دوره اول از ورودی داده ها به شبکه عصبی، وزن های مدل به تعداد 20 مرتبه اصلاح می شوند و در پایان فرآیند یادگیری مدل، وزن های نهایی مدل پس از 20 هزار مرتبه بروزرسانی بدست می آیند.