الگوریتم ماشین بردار پشتیبان SVM با رویکرد یادگیری با نظارت در حل مسائل رده بندی و رگرسیون مورد استفاده قرار می گیرد. البته بیشترین موارد استفاده آن در مسائل رده بندی می باشد و برای اولین بار در سال 1995 توسط Vapnik برای مسئله رده بندی دودویی معرفی شد.
توسعه این الگوریتم برای حل مسائل چند کلاسه، رگرسیون و حتی خوشه بندی (یادگیری بدون نظارت) نیز انجام شده است:
SVR: Support Vector Regression
SVC: Support Vector Clustering
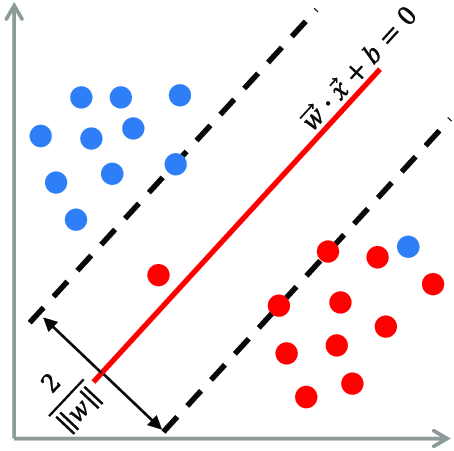
ایده اصلی و متمایز این الگوریتم نسبت به سایر الگوریتم ها، یافتن خط جداکننده و رده بند به شکلی است که حداکثر فاصله از رکوردهای کلاس های هدف را داشته باشد.

فرض کنید مجموعه داده ها شامل بردارهای ,…, } باشد بطوریکه بردار p – بعدی X ویژگی های ورودی مدل و Y فیلد هدف و دارای دو مقدار 1+ و 1- می باشد.
می توان معادله خط (ابرصفحه) جداکننده را به فرم زیر نمایش داد:

این خط (ابرصفحه) مرز تصمیم گیری برای تعلق داده های ورودی به کلاس های فیلد هدف است؛ در الگوریتم SVM به دنبال کاهش ریسک تصمیم گیری از طریق ایجاد بیشترین فاصله خط مرزی با نقاط مرزی کلاس های مجاور می باشد. بنابراین ناحیه تصمیم گیری به فرم زیر نمایش داده می شود، به طوری که فاصله بین دو خط (ابرصفحه) ماکسیمم گردد:
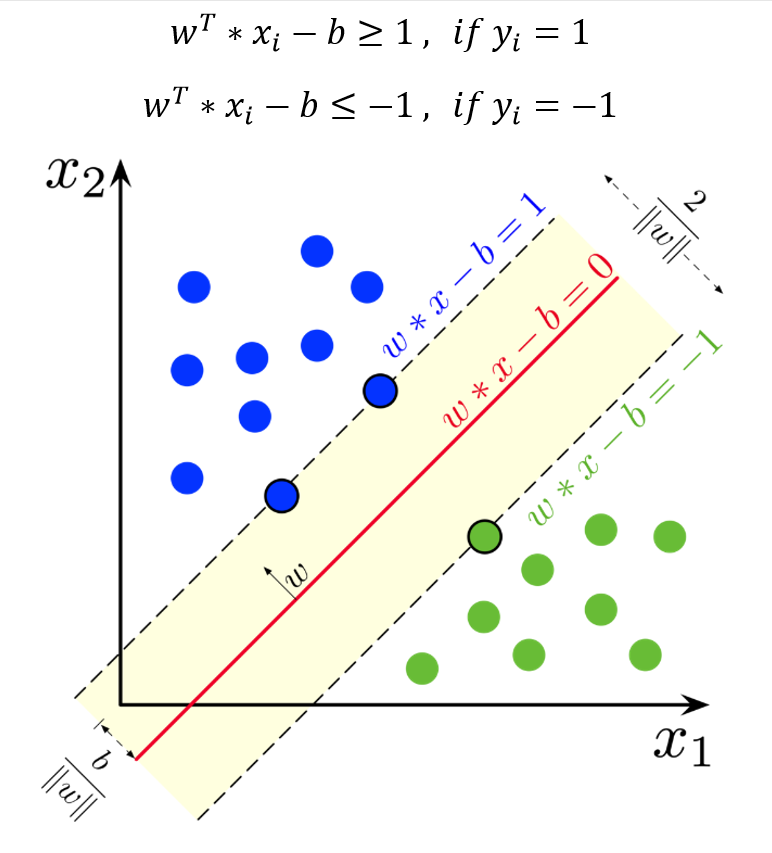
با ضرب مقادیر Y در معادله خطوط مرزی، می توان در قالب یک معادله به شکل زیر نمایش داد:
![]()
بر اساس مفهوم بردار نرمال w در هندسه تحلیلی ثابت می شود، فاصله بین دو خط مرزی که به عنوان حاشیه (Margin) شناخته می شود، برابر با 2 برابر معکوس نرم دوم w می باشد.
با توجه به هدف ماکسیمم کردن این فاصله می توان مسئله را به صورت تابع بهینه سازی زیر در نظر گرفت:
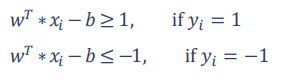
پس از حل مسئله و برآورد مقادیر w و b، مشاهداتی از X که روی خطوط مرزی قرار می گیرند و یا بسیار نزدیک به آنها هستند، بردارهای پشتیبان می گویند.
حاشیه سخت در مقابل حاشیه نرم
در داده های واقعی معمولا به سختی می توان با استفاده از یک خط جداکننده با حاشیه های سخت گیرانه، فاصله های مرزی مطمئنی ایجاد نمود. بنابراین با پذیرفتن مقداری خطا در تصمیم گیری می توان حاشیه های نرم تری برای رده بندی ایجاد نمود:

تابع هزینه (زیان) الگوریتم SVM (Hinge Loss)
برای تعریف تابع هزینه در الگوریتم SVM، برای خطاهای پیش بینی شده طبق رابطه زیر مقدار هزینه (زیان) تعریف می شود:

طبق تعریف تابع هزینه الگوریتم SVM، مقدار هزینه برای خطای پیش بینی، به میزان دور شدن از ناحیه تصمیم مدل، به صورت خطی افزایش می یابد.
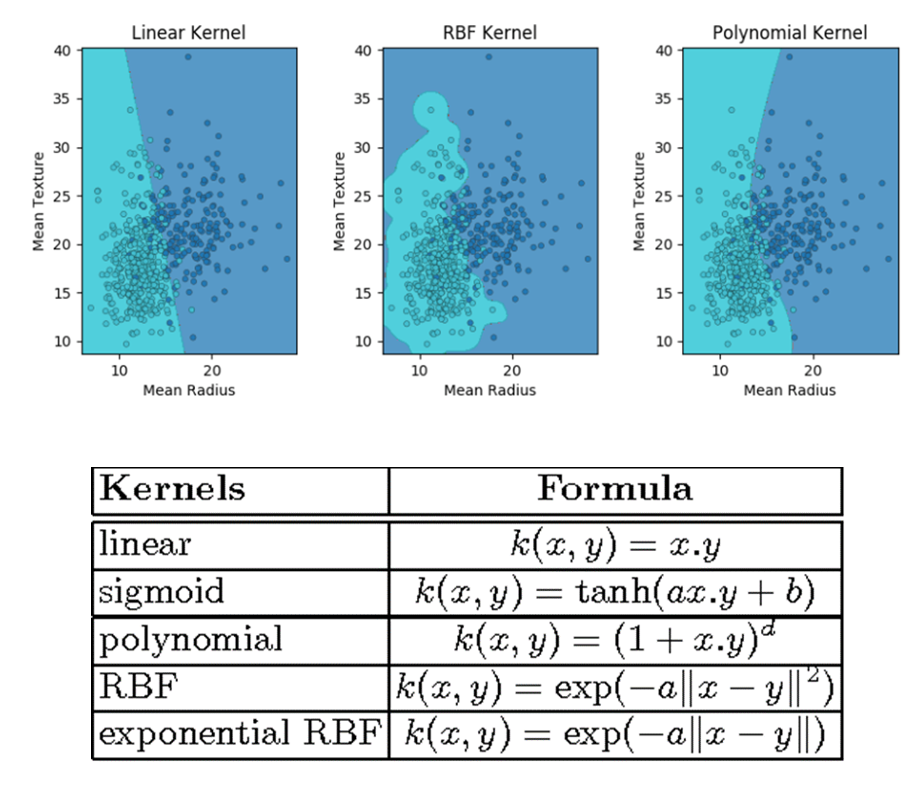
رده بندی الگوهای غیرخطی با استفاده از Kernel
در صورتی که الگوهای موجود در داده ها قابلیت جداسازی بصورت خطی نداشته باشد، با استفاده از توابع تبدیل کرنل جهت نگاشت داده های غیرخطی به فضای ویژگی های جدید به طوری که قابلیت تفکیک خطی داشته باشد، انجام می شود.

در صورتی که الگوهای موجود در داده ها قابلیت جداسازی بصورت خطی نداشته باشد، با استفاده از توابع تبدیل کرنل جهت نگاشت داده های غیرخطی به فضای ویژگی های جدید به طوری که قابلیت تفکیک خطی داشته باشد، انجام می شود. انتخاب تابع کرنل، با بکارگیری توابع مختلف و مقایسه شاخص های ارزیابی انجام می شود.
بنابراین نمی توان بر اساس روش های محاسباتی یا قواعد از پیش تعیین شده، تابع کرنل خاصی را برای یک مجموعه داده یا مسئله تعیین نمود.
بکارگیری روش تنظیم سازی (Regularization term in SVM)
الگوریتم SVM معمولا در مدلسازی داده های با ابعاد بالا و همچنین مجموعه داده هایی که تعداد ویژگی ها بیشتر از رکوردهای آموزشی است، عملکرد خوبی نسبت به سایر الگوریتم ها دارد. بنابراین استفاده از روش های تنظیم سازی برای برآورد ضرایب مدل که منجر به سادگی بیشتر آن می شود، در چنین مسائلی یکی از روش های پر کاربرد می باشد.

به کارگیری الگوریتم SVM در حل مسائل چند کلاسه
الگوریتم های رده بندی دودویی برای حل مسائل چند کلاسه، معمولا از دو رویکرد استفاده می کنند:
● یک در مقابل بقیه (One vs Rest – OvR)
در این حالت مدل رده بند چند کلاسه به تعداد کلاس های فیلد هدف ساخته می شود و هر بار یکی از کلاس ها در مقابل بقیه کلاس ها بصورت مدل دودویی آموزش داده می شود. در نهایت کلاسی که با بیشترین احتمال عضویت بدست آید به عنوان خروجی پیش بینی در نظر گرفته می شود.
این رویکرد عموما در الگوریتم هایی که مقدار احتمال تعلق به یک کلاس را بر می گردانند، مانند الگوریتم های لجستیک یا پرسپترون، مورد استفاده قرار می گیرد و در مواقعی که تعداد رکوردهای مجموعه داده بسیار زیاد باشد، می تواند روش کندی باشد.
● یک در مقابل یک (One vs One – OvO)
در این حالت به تعداد حالت های ممکن تقابل بین کلاس ها، مدل دودویی ساخته می شود و به ازای هر مدل، یک کلاس خروجی یا احتمال تعلق به آن محاسبه می شود. در نهایت با رای گیری روی کلاس های پیش بینی شده توسط تمام مدل هایی دودویی و یا جمع احتمال تعلق هر کلاس در تمامی مدل ها و انتخاب کلاس نهایی بر اساس مقدار ماکسیمم احتمال تجمیعی آن، پیش بینی انجام می شود.
در این حالت تعداد مدل های ساخته شده بیشتر از رویکرد قبلی می باشد، اما به علت انتخاب زیر مجموعه هایی از داده های آموزشی که منجر به کاهش رکوردها می شود، در الگوریتم هایی مانند SVM و یا سایر الگوریتم های مبتنی بر کرنل، بیشتر مورد استفاده قرار می گیرد.