احتمال شاخه ای از علم ریاضی است که عدم قطعیت را بررسی می کند و آمار کار تجزیه و جمع آوری، تحلیل و تفسیر و ارائه اطلاعات مفید از داده ها را در اختیار ما قرار می دهد.
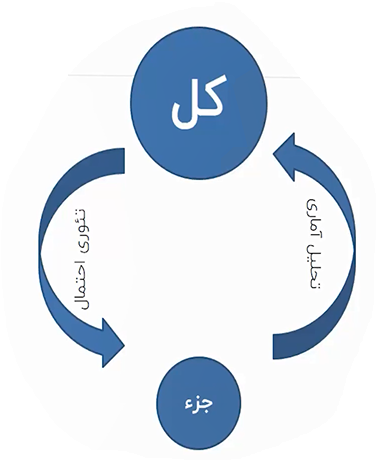
اگر بخواهیم آمار و احتمال را با یکدیگر مقایسه کنیم می توان گفت که این دو در دو جهت متفاوت عمل می کنند؛ در احتمال، یک کل وجود دارد، حقیقتی از یک کل دانسته شده است و سعی بر پاسخگویی به سوالات جزیی از آن احتمال ها است (رویکرد تحلیل احتمال). مثلا توزیع قد مردهای یک جامعه که دارای یک میانگین و واریانس خاص است و مثلا احتمال داشتن قد یک مرد با اندازه خاص در آن جامعه محاسبه می شود.
در تحلیل آماری یک جزء یا بخشی از یک جامعه کل دانسته می شود و سعی بر این است که بتوانیم مشخصات کامل آن مجموعه را محاسبه نماییم. مثلا سمپلی از قد مردان یک جامعه را در اختیار داریم و با محاسبه میانگین و واریانس قد مردان آن جامعه به قد مردان کل آن جامعه تعمیم داده می شود.
در ادامه این مطلب، به توضیح تعدادی از مفاهیم آمار و احتمال خواهیم پرداخت:
جامعه آماری (Population): گروهی از افراد یا اشیا که در ویژگی یا ویژگی های مورد پژوهش مشترک بوده و با هدف و موضوع تحقیق مرتبط باشد.
نمونه (Sample): بخشی از جامعه آماری که مورد مشاهده قرار گرفته است.
آزمایش تصادفی (Random Experiment): آزمایشی که نتیجه آن با اطمینان کامل قابل پیشبینی نباشد. مثلاً نتایج حاصل از پرتاب سکه، ابتلای یک فرد به بیماری و…
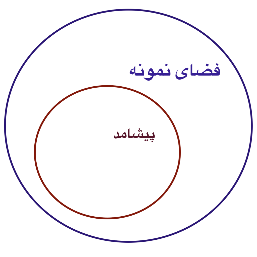
فضای نمونه (Sample Space): مجموعه ای از تمام نتایج ممکن از یک آزمایشی تصادفی؛ مثلا مجموعه نتایج پرتاب یک سکه در دو مرتبه S= {H,T} یا ابتلای یک فرد بیمار کووید 19 {فوت، بهبودی}=S
پیشامد (Event): به هر یک از نتایجی که از یک آزمون بدست می آید اطلاق می شود، به عبارت دیگر به هریک از مجموعه های فضای نمونه پیشامد گفته می شود.
مثلا در مورد مثال پرتاب یک سکه: A={H}, B={T}, C={H,T}, D={}
احتمال(Probability): شاخه ای از ریاضیات که به صورت عددی باور پذیری رخداد یک پیشامد را بیان می کند. برای محاسبه احتمال باید حالت های ممکن را مخرج کسر قرار داد و حالت های مطلوب را در صورت کسر قرار داد.
مثلاً در پرتاب یک سکه: P(A)=P(B)= ½
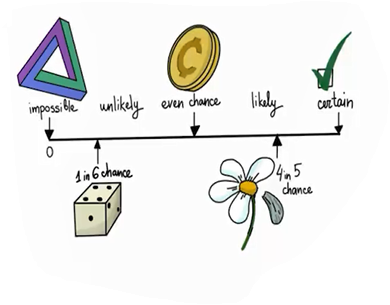
نکته: همیشه احتمال فضای نمونه برابر با یک است.
همیشه احتمال عددی بین صفر و یک است.
انواع تعابیر احتمال:
به طریق شخصی: بر پایه قضاوت و داوری بر اساس اطلاعات و دانسته های قبلی فرد.
به طریق کلاسیک: برپایه مفهوم هم شانس بودن پیشامد های ساده.
به طریق فراوانی نسبی: بر پایه تقریبی از فراوانی نسبی رخداد پیشامد های مورد نظر، در تکرار های زیاد آزمایش تحت شرایط یکسان.