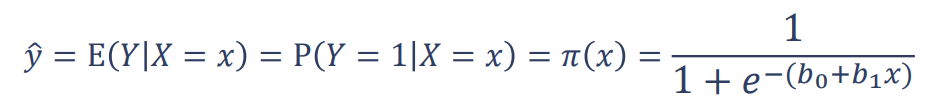رگرسیون لجستیک یکی از الگوریتمهای طبقهبندی (Classification) است که برای اختصاص دادهها به مجموعهای از کلاسها استفاده میشود.
برخی از نمونههای مسائل طبقهبندی عبارتاند از: طبقهبندی ایمیلها به دو دستهی ایمیلهای اسپم (Spam) یا غیر اسپم (Not Spam) یا طبقهبندی معاملات آنلاین به دو دستهی کلاهبرداری یا غیر کلاهبرداری یا طبقهبندی تومورهای بدخیم یا خوشخیم.
همانطور که تا الان متوجه شدیم، بهطور کلی در رگرسیون لجستیک خروجی بهشکل صفر یا ۱ است؛ یعنی برای مثال، یا تومور بدخیم است (1) یا خوش خیم (0).
زمانیکه تعداد کلاسهای خروجی 2 باشد، به آن طبقهبندی باینری (Binary Classification) گفته میشود؛ البته تعداد کلاسهای خروجی میتواند بیشتر هم باشد که در این صورت به آن طبقهبندی مالتی (Multi Classification) گفته میشود.
تا اینجا فهمیدیم که در رگرسیون لجستیک هدف در خروجی اختصاص دادهها به یکی از دو کلاس صفر یا ۱ است. درواقع در این تکنیک احتمال این را که داده به کدام کلاس متعلق است در خروجی خواهیم داشت.
از آنجا که دربارهی احتمال صحبت میکنیم، پس قطعاً میدانیم خروجی ما باید بین صفر و ۱ باشد. حال لازم است ببینیم در اینجا ما به چه تابعی احتیاج داریم که بتواند دادهها را بهخوبی نمایش دهد و در کلاس درستی طبقهبندی کند.
چرا رگرسیون خطی نه؟
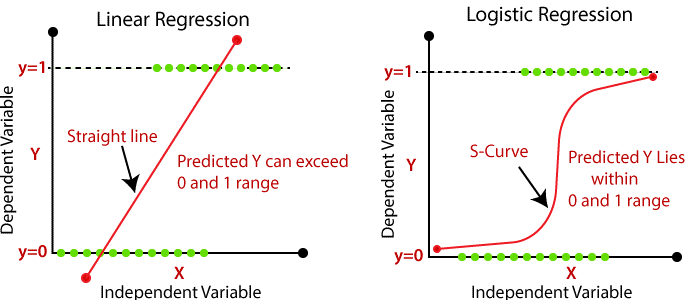
فرض کنید ما مجموعهدادهای داریم که اندازهی تومورها و این امر را که آیا بدخیم هستند یا نه نشان میدهد. اگر این دادهها را روی نمودار ببریم، از آنجا که مسئله طبقهبندی است، تمامی دادهها یا صفر هستند یا یک.
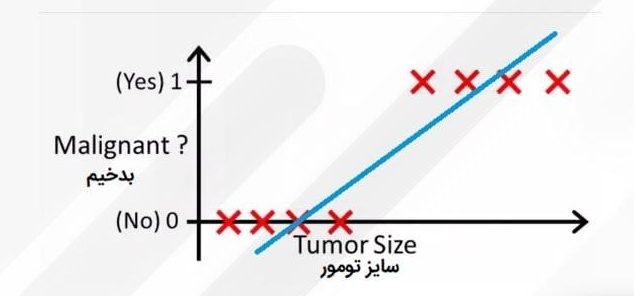
حال اگر از رگرسیون خطی استفاده کنیم، چنین خطی را که در نمودار بالا مشاهده میکنیم به ما میدهد. در اینجا میتوانیم با تعیین یک آستانه (Threshold) در محور x، دادهها را طوری تقسیم کنیم که همهی دادههای موجود در سمت راست آستانهی بدخیم (متعلق به کلاس ۱ یا همان مثبت) و در سمت چپ آن همهی دادههای موجود خوشخیم (متعلق به کلاس صفر یا همان منفی) هستند. در اینجا این آستانه ۰.۵ است.
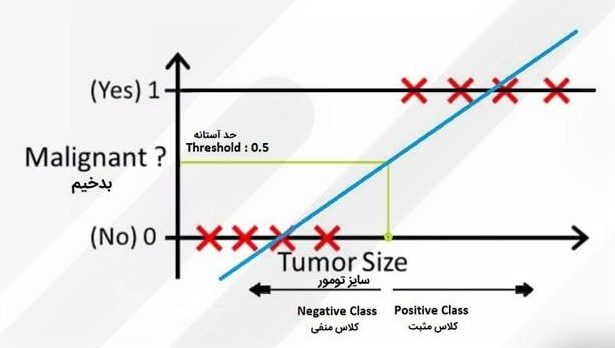
خب، تا اینجای کار رگرسیون خطی خوب جواب داده است و شاید فکر کنیم که اصلاً به رگرسیون لجستیک نیازی نداریم، اما اینطور نیست.
بیایید در نظر بگیریم یک دادهی پرت (Outlier) به این دادهها اضافه شود؛ در این صورت خطی که رگرسیون خطی به ما میدهد بهاین شکل خواهد بود:
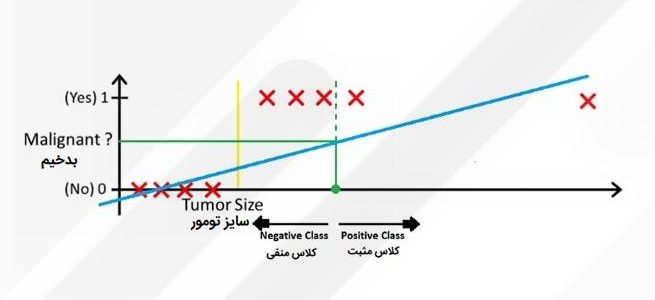
در اینجا اگر بازهی ۰.۵ را بار دیگر بررسی کنیم، میبینیم که دادهها بهدرستی تقسیم نمیشوند؛ خیلی از کلاسهای مثبت را بهاشتباه در دستهی کلاسهای منفی قرار میدهد. درواقع باید بگوییم بار اول رگرسیون خطی بهصورت اتفاقی دادهها را به درستی تقسیم کرد؛ پس بههمین دلیل، ما به رگرسیون لجستیک نیاز داریم.
چرا به رگرسیون لجستیک (Logistic Regression) نیاز داریم؟
همانطور که میدانیم، در رگرسیون خطی ما باید به بهترین معادلهی خطی میرسیدیم تا دادهها را بهدرستی نمایش دهد. این را در نظر بگیریم که در رگرسیون خطی معادلهی خطی میتواند هر مقداری داشته باشد، درحالیکه در طبقهبندی و رگرسیون لجستیک (Logistic Regression) مقادیری که در خروجی داریم احتمال تعلق داده به یکی از دو کلاس صفر یا ۱ است؛ بنابراین مقادیر باید میان صفر و ۱ باشد که این موضوع با معادله خطی امکانپذیر نیست.
پس ما به معادلهی دیگری احتیاج داریم که آن تابع سیگموید یا همان لجستیک (Sigmoid/ Logistic Function) است.
تابع سیگموید بهاین شکل است:
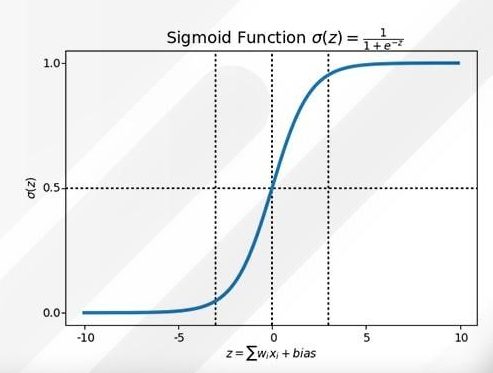
معادلهی خطیمان در رگرسیون خطی بهاین شکل بود:
Z = β₀ + β₁X
در رگرسیون لجستیک معادلهی ما بهاین شکل خواهد بود:
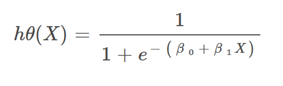
یعنی همان سیگموید معادلهی خطی خواهد بود که در رگرسیون خطی داشتیم.
قبل از اینکه ببینیم چطور پارامترهای این معادله را بهینه میکنیم، بیایید دربارهی مرز تصمیمگیری (Decision Boundary) صحبت کنیم.
یکی از انواع الگوریتم های با یادگیری با نظارت از نوع رده بندی می باشد که بر خلاف رگرسیون خطی به دنبال بررسی رابطه و مدلسازی ویژگی های ورودی مستقل با فیلد هدف (پاسخ) از نوع کیفی می باشد.
یکی از انواع الگوریتم های با یادگیری با نظارت از نوع رده بندی می باشد که بر خلاف رگرسیون خطی به دنبال بررسی رابطه و مدلسازی ویژگی های ورودی مستقل با فیلد هدف (پاسخ) از نوع کیفی می باشد.
با توجه به توزیع برنولی فیلد هدف خواهیم داشت:
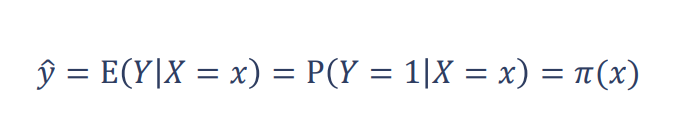
بر اساس رابطه فوق، مقدار پیش بینی برای برای فیلد هدف، بایستی مقدار احتمال در بازه 0 تا 1 باشد.
تابع لجستیک (سیگموید) Logistic (Sigmoid) Function
تابع سیگموید (Sigmoid function) یک تابع ریاضی است که شکلی مشابه با حرف S در زبان انگلیسی دارد. به طور کلی به توابعی که شکل آنها مشابه با حرف S است تابعهای سیگموید یا دارای خمیدگی سیگموید میگویند.
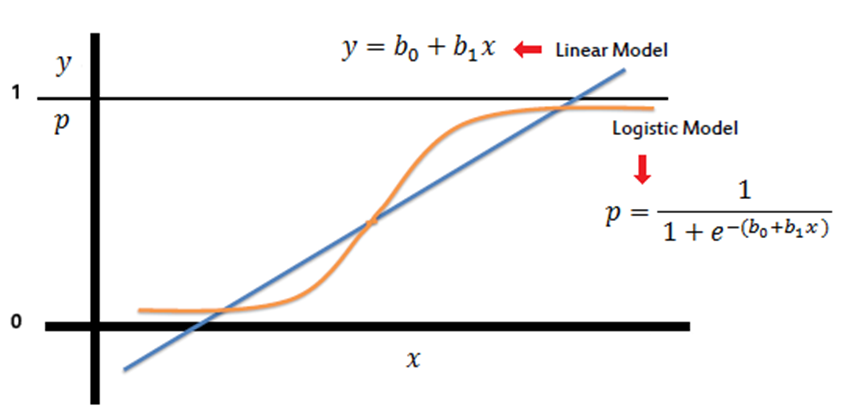
با توجه به اینکه مقدار𝜋(𝑥) در بازه 0 تا 1 قرار می گیرد، بنابراین نیاز است جهت پیش بینی مقدار y از تابعی مانند تابع لجستیک استفاده شود تا مقدار خروجی در بازه 0 تا 1 قرار گیرد. تابع لجستیک برای خط رگرسیون ساده به شکل زیر تعریف می گردد:
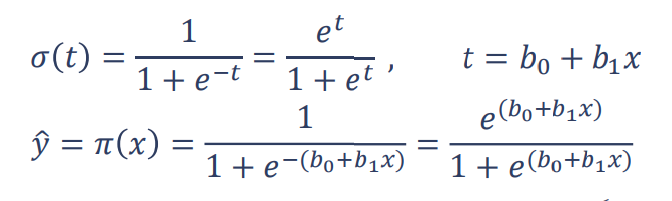
با توجه به پیچیدگی نمایش مدل برآورد y، علاقمند هستیم با تبدیل های مناسب نمایش آن را ساده تر کنیم. به این منظور از مفهومی به نام بخت (Odds) استفاده می کنیم.
مفهوم بخت (Odds)
محاسبه بخت بر اساس نسبت احتمال وقوع به احتمال عدم وقوع انجام می شود. بنابراین مقدار بخت، بر خلاف مقدار احتمال می تواند بزرگتر از یک نیز باشد. بطور مثال فرض کنید احتمال خوش خیم بودن غده سرطانی برای یک شخص 0.75 برآورد شده است، بنابراین مقدار بخت برای این فرد 3 می باشد.
با توجه به این مفهوم روابط زیر را خواهیم داشت: 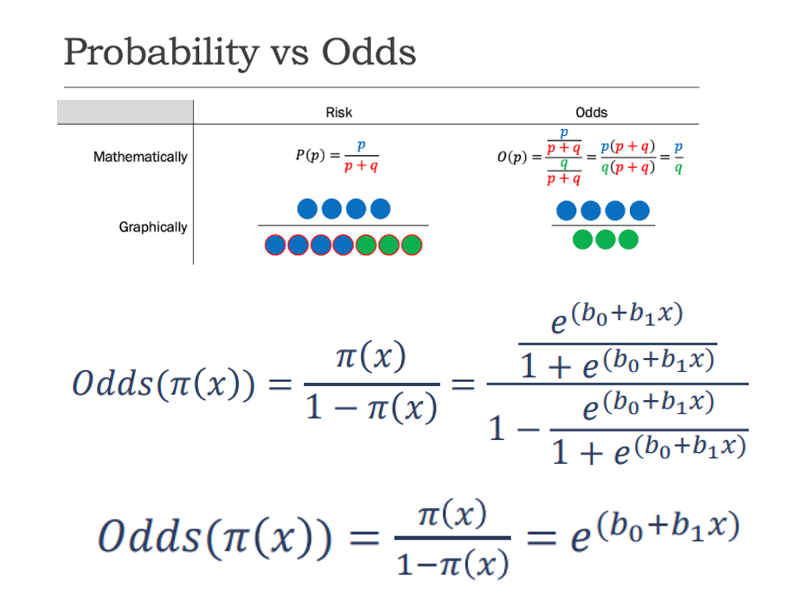
تبدیل لوجیت (Logit Transformation)
لگاریتم طبیعی بخت به عنوان تبدیل لوجیت یا بعضا (Log-Odds) شناخته می شود. در رگرسیون لجستیک با استفاده از تبدیل لوجیت بر روی احتمال وقوع x (برآورد مقدار y) می توان رابطه خطی رگرسیون را به شکل زیر نمایش داد.

پس از برآورد ضرایب مدل بر اساس روش حداکثر درستنمایی (MLE) در رگرسیون لجستیک، بر خلاف رگرسیون خطی، مقدار y بصورت مستقیم برآورد نمی شود. بلکه مقدار Logit(𝑦 ̂) به صورت ترکیب خطی از ویژگی های ورودی محاسبه شده و مقدار احتمال کلاس یک (کلاس مبنا) برای تصمیم گیری و رده بندی استفاده می شود.