مجدداً به مثال مطالعه‌ی موردی خرده‌فروشی دایکه برای تحلیل‌های بازاریابی خوش آمدید. در ۸ بخش قبلی، برخی از وظایف کلیدی علم داده مثل موارد زیر را مطرح کردیم:
توصیف: بخش ۳
تحلیل وابستگی: بخش ۴
دسته‌بندی: بخش ۵، بخش۶، بخش ۷ و بخش ۸
در این بخش، راجع به برآورد ازطریق مادر همه‌ی مدل‌ها، یعنی رگرسیون خطی چندگانه یاد می‌گیریم. درک عمیقی از تحلیل رگرسیون و مدل‌سازی، پایه‌ی محکمی برای تحلیل‌گران مهیا می‌سازد تا کمابیش شناخت عمیق‌تری از سایر روش‌های مدل‌سازی، مثل شبکه‌های عصبی، رگرسیون لجستیک و غیره کسب کنند. اما پیش از مبحث رگرسیون اجازه دهید با استفاده از پرطرفدارترین رویداد المپیک تابستانی، تدابیر اساسی ماورای آمار را مطرح و مقایسه کنیم.
دو ۱۰۰ متر
اولین بازی‌های المپیکی که در سال ۱۹۸۸ دنبال کردم در سئولِ کره‌ی جنوبی برگزار می‌شدند. این همان المپیکی بود که بن جانسون[1] رکورد جهانی دو ۱۰۰ متر آن زمان را با رسیدن به نقطه‌ی پایان در عرض ۹.۷۹ ثانیه شکست. بعدها، نتیجه‌ی آزمایش استعمال داروهای تقویت عملکرد توسط جانسون مثبت اعلام شد. جانسون رد صلاحیت و از مدال محروم شد. برای رویدادی ورزشی که فقط ۱۰ ثانیه طول می‌کشد، دو ۱۰۰ متر یقیناً پرطرفدارترین رویداد المپیک تابستانی بود. در المپیک ۲۰۱۲، اُسین بولت[2] با رسیدن به نقطه‌ی پایان در عرض ۹.۶۳ ثانیه، رکورد جدیدی ثبت کرد. جدول زیر، لیست برندگان مدال المپیک ۲۰۱۲ را ارائه می‌دهد (منبع: ویکیپدیا).
اُسین بولت به‌عنوان سریع‌ترین مرد جهان شناخته می‌شود. هرچند، باید بگویم که…
شما می‌توانید اُسین بولت را در دو ۱۰۰ متر شکست دهید!
پیش از آن‌که توضیح بدهم چطور می‌توانید این کار را بکنید، اجازه دهید به مدال‌گیرندگان المپیک ۲۰۱۲ برگردیم. برای مثال، اگر اُسین بولت را مجبور کنیم هزار بار دو ۱۰۰ متر را بدود، او هر دور را با زمان‌بندی متفاوتی به پایان می‌رساند؛ بیشتر نزدیک به زمان رکوردش در المپیک. همین امر برای سایر مدال‌گیرندگان، یوهان بلیک و جاستین گاتلین هم واقعیت دارد. به‌خاطر ماهیت بحث، توزیع‌های زیر را برای زمان رسیدن به خط پایان هر سه مدال‌گیرنده فرض می‌گیریم. توزیع‌های زیر همگی نرمال یا گوسی هستند. توزیع نرمال فرضیه‌ی خوبی برای بیشتر پدیده‌های طبیعی مثل دویدن با سرعت انسان‌ها است.
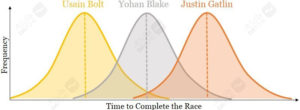
طبق توزیع‌های بالا، مدال طلا هنوز هم به اُسین بولت، به‌عنوان محتمل‌ترین برنده، تعلق میگیرد. هرچند، هنوز هم مواردی هستند که در آنها قهرمان دو سرعت می‌تواند برنده‌ی مدال طلا نشود. این امر، به عقیده‌ی من، اساس اندیشیدن آماری است.
حالا به عنوان این بخش برمی‌گردیم، اگر گوگل۱۰ بار با اُسین بولت مسابقه دهید، پس احتمالش هست که دست‌کم یکی از این مسابقات درمقابل سریع‌ترین مرد جهان را ببرید. آره!
تحلیل رگرسیون – مثال مطالعه‌ی موردی خرده‌فروشی
حالا اجازه دهید به مثال مطالعه‌ی موردی‌مان برگردیم؛ در این مثال، شما مدیر ارشد تحلیل و رئیس راهبرد کسب‌وکار در فروشگاه آنلاینی به‌نام شرکت درس‌اسمارت هستید که دو هدف دارد:
هدف ۱: ارتقاء نرخ تبدیل کمپین‌ها، یعنی تعداد مشتریانی که از کاتالوگ بازاریابیِ محصولات خرید می‌کنند.
هدف ۲: ارتقاء سود حاصل‌شده ازطریق مشتریان تبدیل‌شده.
در چند بخش قبلی این مثال مطالعه‌ی موردی به هدف اول رسیدید. از مدل‌های دسته‌بندی (بخش‌های ۵، ۶، ۷ و ۸) برای برآورد تمایلات مشتریان در واکنش به کمپین‌ها استفاده کردید. پس هدف دوم می‌ماند که مختص برآورد سود موردانتظار تولیدشده از هر مشتری‌ای است که به کمپین واکنش نشان می‌دهد. این مسئله‌ی رگرسیون کلاسیک است. برای توسعه‌ی مدل رگرسیون، از داده‌های مربوط به ۴۲۰۰ مشتری از بین صدها هزار مشتری متقاضی، یعنی مشتریانی که به کمپین‌های قبلی پاسخ داده‌اند، استفاده خواهید کرد. این ۴۲۰۰ مشتری در مکان‌های مختلفی زندگی می‌کنند که می‌توان آنها را به سه دسته‌ی زیر تقسیم‌بندی کرد:
۱. شهرهای بزرگ
۲. شهرهای متوسط
۳. شهرهای کوچک
این مشتریان برحسب اتفاق به طور مساوی در این سه دسته تقسیم میشوند و ۱۴۰۰ مشتری در هر گروه جای میگیرد.
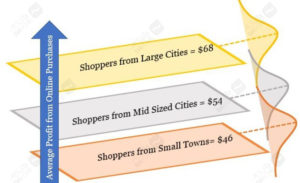
اولین چیزی که بررسی میکنید، مقدار سود حاصل از این سه دسته شهر است. همانطور که در شکل روبهرو میبینید، مقادیر متوسط سود این سه دسته متفاوتند. این مقادیر متوسط را به‌خاطر بسپرید، چون هنگام توسعه‌ی مدل رگرسیون به‌‌دردمان می‌خورند.
حالا سؤال دوم این است که آیا این مقادیر متوسط تفاوت قابل‌توجهی دارند یا نه.این پرسش را می‌توان با استفاده از توزیع‌های مربوط به دسته‌ی مکانی کل ۴۲۰۰ مشتری پاسخ داد. شکل بالا نمایشی از این توزیع‌ها (به سمت راست) را ارائه می‌دهد. برای داده‌های اصلی‌مان، شکل زیر توزیع تراکم مربوط به دسته‌ی مکانی کل این ۴۲۰۰ مشتری را ارائه می‌دهد. توجه کنید که سود به‌خاطر کالاهای برگشتی توسط مشتریان و سایر زیان‌ها، در برخی موارد در این توزیع منفی است.
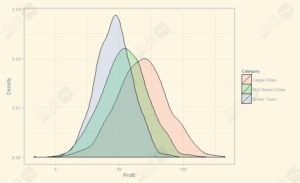
چندین بینش شهودی در نمودارهای بالا وجود دارد:
۱. مقادر متوسط سود شهرهای بزرگ، به‌دلیل ظرفیت درآمدزایی بالاتر و درآمد قابل‌عرضه برای ساکنین کلان شهرها در مقایسه با سایر شهرها بالاتر است.
۲. شهرهای بزرگ همچنین به‌خاطر تنوع اقتصادی-اجتماعی بیشتر کلان شهرها، در مقایسه با دو دسته‌ی دیگر توزیع سود گسترده‌تری دارند.
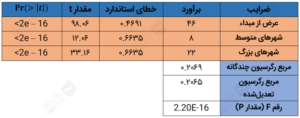
دو بینش بالا را به خاطر بسپرید و بیایید مدل رگرسیون ساده‌مان را با این دو دسته، به‌عنوان متغیرهای پیش‌بین بسازیم. جدول زیر، نتایج مدل رگرسیون را ارائه می‌دهد:
معادله‌ی زیر، معادله‌ی خطی این مدل رگرسیون است:
توجه کنید که متغیرهای پیش‌بین این مدل فقط شهرهای بزرگ و متوسط هستند. اطلاعات مربوط به شهرهای کوچک در بخش عرض از مبداء جذب میشوند. به‌علاوه، این متغیرهای پیش‌بین، متغیرهایی ساختگی هستند، پس تنها مقادیری که می‌توان به آنها داد ۰ و ۱ است. برای مثال، اگر مکان شهری کوچک باشد، پس مقدار شهرهای متوسط، ۰ و مقدار شهرهای بزرگ هم ۰ است و درنتیجه سود ۴۰ می‌شود:
اگر مقادیر متوسط را به‌یاد آورید، میبینید که این مقدار همان مقدار متوسط شهرهای کوچک است. حالا، اگر مکان شهری متوسط باشد، پس:
حالا سؤال بعدی که پیش می‌آید این است: این مدل چقدر خوب است؟ برای پاسخ‌گویی به این پرسش باید نتایج مدل رگرسیون را بالا پایین کنیم و سه مورد زیر را بررسی نماییم:
۱. مقادیر P ضرایب تکی: به سمت‌راست‌ترین ستون ضرایب نگاهی بیندازید؛ مقدار واقعاً کوچک است، <2e – 16، این بدان معنی‌ست که مدل تقریباً ۱۰۰ درصد مطمئن است که ضرایت ۰ نخواهند شد. این شبیه شانس شما در شکست‌دادن اُستین بولت است، یعنی شدیداً پایین، اما نه صفر.
۲. مقدار مربع رگرسیون تعدیل‌شده: برای مدل ما این مقدار ۰.۲۰۶۵ است. این بدان معنی‌ست که فقط دسته‌ی مکانی حدود ۲۰ درصد از اختلاف در سود را توجیه می‌کند. درصورتی‌که افزودن متغیرهای معنی‌دارتر به مدل بالا را همچنان ادامه دهیم، مقدار مربع رگرسیون تعدیل‌شده افزایش خواهد یافت و این برای متغیر دسته‌ای تکی بد نیست.
۳. ارقام F: باز هم می‌گویم که مقدار P در اینجا خیلی کوچک است، یعنی 2.20E-16. این بدان معنی‌ست که شانس این مدل در تصادفی‌بودن خیلی پایین است، مثل شانس شما در شکست‌دادن تصادفی اُستین بولت.
مخلص کلام
اظهارات زیر، حقایق کلی ضروری ماورای بازی‌های المپیک را جمع‌بندی می‌کنند. مهمترین چیز در بازی‌های المپیک برنده‌شدن نیست، بلکه شرکت‌کردن است. امر ضروری پیروزی نیست، بلکه نبرد خوب است.
پس وارد عرصه شوید، خوب بازی کنید و از همه مهمتر لذت ببرید، حتی اگر رقیب‌تان سریع‌ترین مرد جهان است. تا بعد!
[1] Ben Johnson
[2] Usain Bolt
