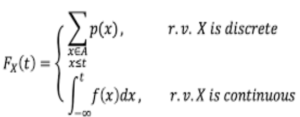در بخش قبلی این مقاله، تعدادی از توزیع های پرکاربرد در مباحث آماری را مطرح کردیم. در این مقاله به ادامه این روند می پردازیم و توزیع های دیگری را معرفی خواهیم کرد:
توزیع T
توزیع t نیز مانند توزیع نرمال قرینه است ولی دارای پراکندگی بیشتری نسبت به توزیع نرمال است و برای مقادیر مختلف حجم نمونه (n) میزان پراکندگی توزیع t تغییر می کند و با افزایش حجم نمونه این پراکندگی کمتر شده و توزیع t با توزیع Z برابر می شود.
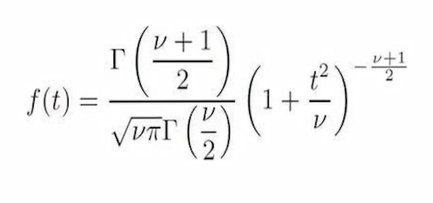
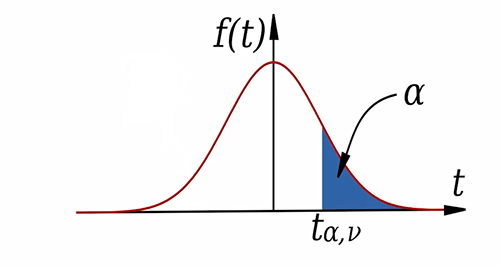
برای استفاده از جدول t احتیاج به دو عدد سطح منحنی در دنباله سمت راست توزیع و درجه آزادی توزیع tداریم.
مثال: مثلا هر گاه بخواهیم بگوییم توزیع t داریم که درجه آزادی آن 5 است و میخواهیم بدانیم کدام چندک احتمال سمت راستش 0.25 است در جدول اعداد 5 و 0.25 را به هم وصل می کنیم که میبینیم در 2.571 این اتفاق رخ داده است.
توزیع کای-دو
این توزیع نیز در مقادیر مثبت x تعریف می شود و بر خلاف توزیع نرمال یک توزیع چوله (Skewed) است و فقط درجه آزادی پارامتر مجهولش است. (=r درجه آزادی)
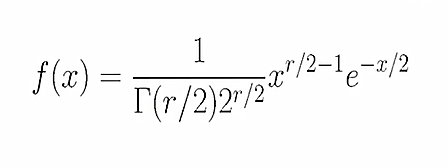
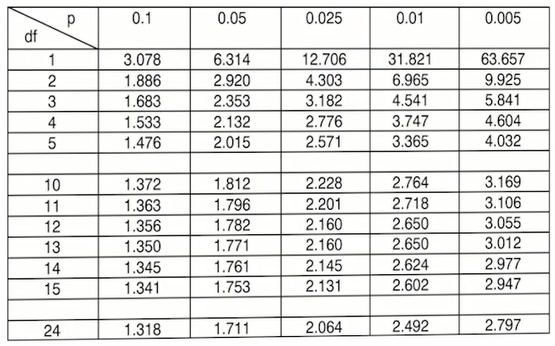
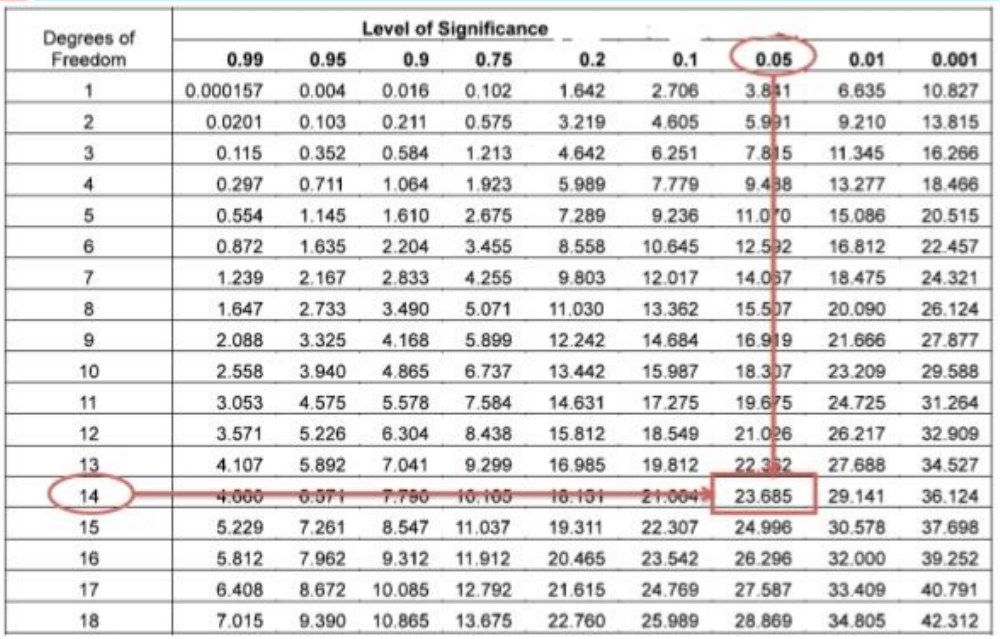
مثلا اگر به دنبال چندکی هستیم که احتمال سمت راست ان 0.05 بشود که درجه ازدی آن هم 14 باشد از جدول مربوط به این توزیع استفاده می کنیم.
توزیع F
توزیع F هم مشابه با توزیع کای-دو یک توزیع چوله (Skewed) است و متقارن نیست و روی اعداد مثبت تعریف می شود. تفاوت آن با توزیع کای-دو در این است که وابسته به دو پارامتر درجه آزادی اول و دوم است.
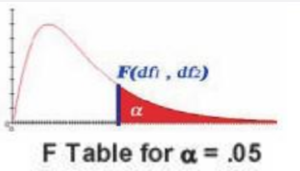
با توجه به اینکه در این توزیع 3 پارامتر درجه آزادی یک و دو و میزان احتمال (α) را داریم جداول آن به نوعی سه بعدی خواهد بود و در نتیجه حجم بیشتری نسبت با آنچه تا کنون دیده ایم دارد.
به عنوان مثال در اگر بخواهیم در احتمال 0.05 چندکی را بخواهیم بدست بیاوریم که درجه های آزادی آن به ترتیب 9 و 15 باشد مشابه جدول زیر عمل می کنیم.
توزیع یکنواخت
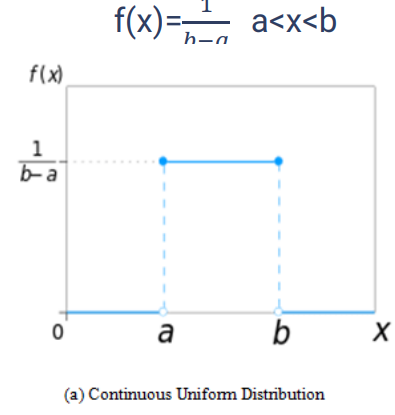
توزیع یکنواخت به صورت یک خط صاف و یا نقطه ای دیده می شود. این توزیع برای داده های گسسته و پیوسته کاربرد دارد.
در تصویر زیر احتمال ها به صورت یکنواخت تغییر می کنند و تنها در بعضی از مقادیر دارای تغییر هستند؛ به عنوان مثال احتمال a تا a+x<b یکسان است و تغییر ندارد تا جایی که مقدار به b تغییر کند.
همینطور برای حالت های گسسته هم همینطور است، مشابه تصویر زیر، اگر n تا event داشته باشیم همه آن ها با احتمال 1/n اتفاق می افتد؛ مثل پرتاب تاس که هر عدد با احتمال 1/6 است.
توزیع پواسون
توزیعی برای شمارش رخداد و اتفاق های نادر، مثلا تعداد اشتباهات تایپی در یک صفحه، تعداد تماس های اشتباه و… معمولا برای توزیع یک مکان و زمان نیز در نظر گرفته می شود.
در فرم بسته تابع توزیع پواسون پارامتر مجهول λ است که برابر است با نقطه تمرکز یا همان وسط توزیع و به عبارت دیگر به آن امید ریاضی میگویند.
در شکل نمونه زیر میبینیم که هرچقدر λ افزایش پیدا کرده میانگین توزیع یا مرکزیت توزیع به سمت جلو پیش می رود و هر چقدر که شده است توزیع متقارن نزدیکتر می شویم
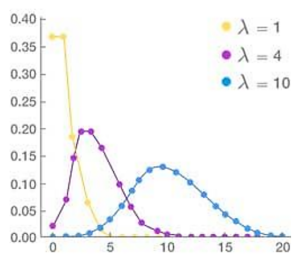
ارتباط بین توزیع پواسون و توزیع دو جمله ای
در هر لحظه از توزیع پواسون ، توزیع دو جمله ای داریم، فرض کنید که میخواهیم تعداد تصادفات را حالی که از پنجره به بیرون نگاه می کنیم بشماریم، می شود در هر ثانیه اتفاقی بیافتد یا نیافتد ( ثانیه اول، ثانیه دوم و…) یعنی در هر x میتواند اتفاقی که منتظر آن بودیم (مثلا پیروزی) رخ دهد یا ندهد. یعنی n به عنوان تعداد لحضات خیلی زیاد است اما احتمال رخ دادن اتفاق خیلی کم است.
در توزیع دوجمله ای امید ریاضی np بود، بنابر این در توزیع پواسون λ=np است
در آمار و احتمال توزیع پواسون (یا قانون پواسون اعداد کوچک) یک توزیع احتمالی گسسته است که احتمال اینکه یک حادثه به تعداد مشخصی در فاصله زمانی یا مکانی ثابتی رخ دهد را شرح می‌دهد؛ به شرط اینکه این حوادث با نرخ میانگین مشخصی و مستقل از زمان آخرین حادثه رخ دهند.
توزیع پواسون همچنین برای تعدادی از حوادث در فاصله‌های مشخص دیگری مثل مسافت، مساحت یا حجم استفاده شود.
توزیع نمایی
در توزیع پواسون شمارش اتفاق های نادر مد نظر است اما در توزیع نمایی زمان تا اتفاق افتادن آن اتفاق نادر مد نظر است. مثلا اینکه یک لامپ را روشن می کنیم، زمان تا سوختن لامپ مد نظر است. در توزیع نمایی مرکزیت یا میانگین توزیع (امیدx) برابر است با
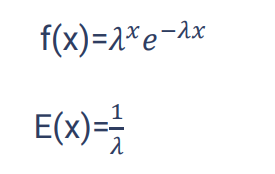
در توزیع نمایی خاصیت عدم حافظه وجود دارد؛ یعنی مهم نیست که افتاق قبلی چه زمانی اتفاق افتاده است یا نیافتاده است و هر پیشامد گویی که یک پیشامد جدید است. عملا زمان تا رخداد اول ارتباطی بین زمان تا رخداد دوم وجود ندارد.
ارتباط بین توزیع پواسون و توزیع نمایی
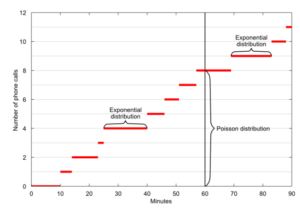
برای مثال شما به دفتر کار خود می‌رسید و می‌بینید که مدیرتان با تلفن صحبت می‌کند. با خود این سوال را می‌پرسید که تلفنِ او چند دقیقه‌ی دیگر تمام می‌شود؟ یا پلیسی که وسط یک نزاع خیابانی سر میرسد و با خود می‌گوید چند ثانیه دیگر این درگیری تمام می‌شود؟
یا حتی پاسخ به این سوال که چند وقت دیگر در فلان منطقه زلزله می‌شود؟ چون این فرآیندها و بسیاری از فرآیند‌های دیگر، توسط تابع نمایی مدل‌سازی می‌شوند، پاسخ به این سوالات نیز توسط توزیع نمایی انجام می‌شود.
توزیع نمایی از یک قاعده‌ی کلی پیروی می‌کند. رویدادهای کوچک، بسیار زیاد اتفاق می‌افتند و رویدادهای بزرگ، به ندرت و کم اتفاق می‌افتند. مثلاً در مورد زلزله، تعداد زیادی زلزله با ریشتر کم اتفاق می‌افتد ولی چند موردِ معدود زلزله با ریشتر بسیار بالا رخ می‌دهد. یا مثلاً در تماس‌های تلفنیِ یک منشی، تعدادِ زیادی مکالمه‌ی کوتاه مدت وجود دارد و تعداد کمی مکالمه‌ی بلند مدت.
تابع توزیع تجمعی
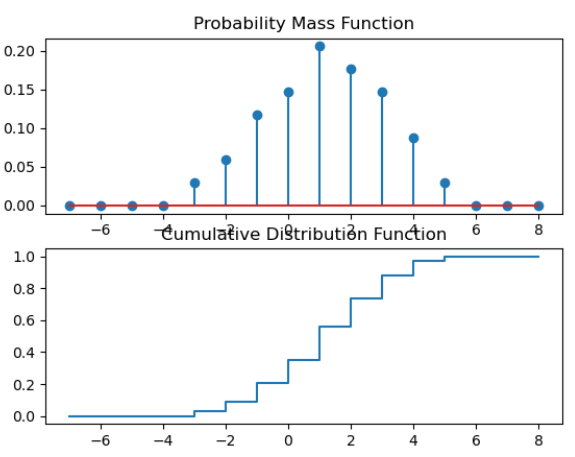
این تابع احتمال را به صورت تجمعی تا نقطه ای خاص حساب می کند. در نهایت در نمودار های تابع توزیعی عدد به نزدیک یک میرسد. در حالتی که متغیر تصادفی گسسته باشد نمودار به شکل پلکانی در می آید.
