آمار توصیفی
خالص سازی داده های نمونه با روش هایی نظیر جداول فراوانی، نمودارها و شاخص های آماری.
در آمار توصیفی از دو ابزار برای ترسیم یا گزارش ویژگی های موجود در داده ها استفاده می شود:
- جداول آمار: متشکل از شاخص های آماری است.
شاخص های پراکندگی
شاخص های مرکزی
- نمودار های آماری : انواع مختلفی دارد و بنا به نوع داده ها و اهداف محقق مورد استفاده قرار میگیرد.
آمار استنباطی
مجموعه ای از روش های آماری كه بر اساس اطلاعات حاصل از نمونه استنباط هایی در باره جامعه آماری به دست می آید.
آمار استنباطی چیست؟
آمار استنباطی Inferential statistics روشی برای قضاوت پیرامون پارامتر جامعه براساس مقادیر حاصل از نمونه است. در مطالعات مختلف به دلایل متفاوت دستیابی به همه افراد جامعه امکان پذیر نیست بنابراین لازم است تا با استفاده از نمونه به تخمین اندازههای واقعی در جامعه پرداخت.
به بیان دیگر، در پژوهشهای روانشناسی و سایر علوم رفتاری کسب اطلاعات درباره گروههای کوچک غالبا هدف پژوهشگر نیست، بلکه او علاقمند است که از طریق یافتههای این گروه کوچک، اطلاعات لازم را درباره جامعهای که این گروه کوچک را از آن انتخاب کرده است، کسب کند. یعنی در این پژوهشها هدف پژوهشگر تعمیم نتایج بهدستآمده از یک گروه کوچک به یک جامعه بزرگتر میباشد.
این تعمیم مستلزم آن است که پژوهشگر از روشهای آماری پیشرفتهتری تحت عنوان استنباط آماری Statistical inference استفاده نماید. چنانچه به جای مطالعه کل اعضای جامعه، بخشی از آن با استفاده از فنون نمونهگیری انتخاب شده، و مورد مطالعه قرار گیرد و بخواهیم نتایج حاصل از آن را به کل جامعه تعمیم دهیم از روشهایی استفاده میشود که موضوع استنباط آماری است.
بنابراین مفاهیم جامعه و نمونه در قلب این روش قرار دارد. آن چه که مهم است این است که در گذر از آمار توصیفی به آمار استنباطی یا به عبارت دیگر از نمونه به جامعه بحث و نقش احتمال شروع میشود. در واقع احتمال، پل رابط بین آمار توصیفی و استنباطی به حساب میآید.
آمار استنباطی و آمار توصیفی
بطور کلی آمار استنباطی در برابر آمار توصیفی قرار میگیرد. در یک پژوهش جهت بررسی و توصیف ویژگیهای عمومی پاسخ دهندگان از روش های موجود در آمار توصیفی مانند جداول توزیع فراوانی، در صد فراوانی، درصد فراوانی تجمعی و میانگین استفاده میگردد.
بنابراین هدف آمار توصیفی یا descriptive محاسبه پارامترهای جامعه با استفاده از سرشماری تمامی عناصر جامعه است. در آمار استنباطی یا inferential پژوهشگر با استفاده مقادیر نمونه آماره ها را محاسبه کرده و سپس با کمک تخمین و یا آزمون فرض آماری، آماره ها را به پارامترهای جامعه تعمیم می دهد.
برای تجزیه و تحلیل داده ها و آزمون فرضیه های پژوهش از روش های آمار استنباطی استفاده می شود. پارامتر شاخص بدست آمده از جامعه آماری با استفاده از سرشماری است و شاخص بدست آمده از یک نمونه n تائی از جامعه آماره نامیده می شود.
برای مثال میانگین جامعه یا µ یک پارامتر مهم جامعه است. چون میانگین جامعه همیشه در دسترس نیست به همین خاطر از میانگین نمونه یا X̄ که آماره برآورد کننده پارامتر µ است در بسیاری موارد استفاده می شود.
مقیاس های اندازه گیری
- مقیاس های اسمی (Nominal Scales): مانند رنگ محصول و گروه خونی – کیفی
- مقیاس های رتبه ای (Ordinal Scales): مانند سطح تحصیالت و سطح رضایت – کیفی
- مقیاس های عددی (Numerical Scales): سن و فشار خون – کمی
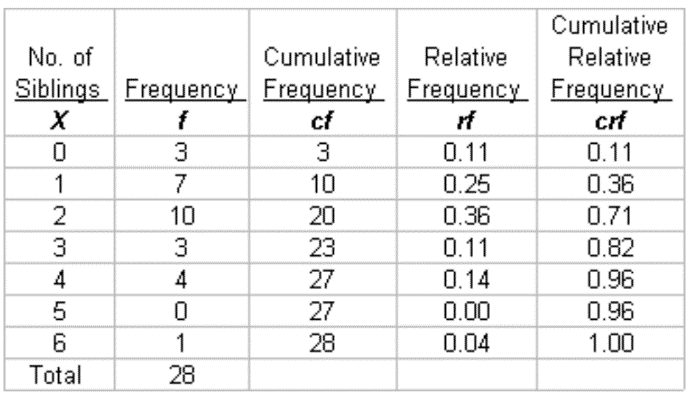
شاخص های جدول فراوانی
- فراوانی (مطلق): به تعداد دفعاتی که یک داده آماری در یک جامعه آماری تکرار می گردد فراوانی مطلق گفته و آن را با Fi نشان می دهیم.
- فراوانی تجمعی: منظور از فراوانی تجمعی طبقه i ام یعنی مجموع فراوانی های مطلق از طبقه اول تا طبقه i ام که آن را با fci نشان میدهیم.
- فراوانی نسبی: عبارت است از خارج قسمت فراوانی مطلق هر دسته یا طبقه بر حجم جامعه که آن را با fi نشان داده و از رابطه زیر محاسبه می گردد.
- فراوانی نسبی تجمعی: عبارت است ازخارج قسمت فراوانی تجمعی هر دسته یا طبقه بر حجم جامعه.
شاخص های مرکزی
- میانگین (mean): حاصل جمع اعداد تقسیم بر تعداد
- میانه (median): نقطه وسط داده ها. زمانی که دیتا ها چولگی دارد بهتر است برای توصیف داده ها از میانه استفاده کنیم.
- شاخص مد (نما): رده ای که بیشترین فراوانی را دارد. در داده های پیوسته باید از استفاده از این شاخص دقت زیادی شود.

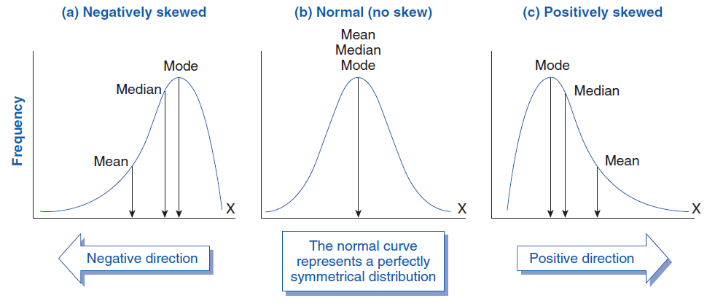
چولگی(Skewness)
نشان دهنده میزان عدم تقارن توزیع احتمالی است. اگر دادهها نسبت به میانگین متقارن باشند، چولگی برابر صفر خواهد بود. چولگی وقتی پیش میاید که دیتا ها متقارن نباشند. در این توزیع ها ما چولگی راست و چپ داریم
کشیدگی (Kurtosis)
توصیف کننده میزان قلهای بودن و مسطح بودن یک توزیع احتمالی است. هر چقدر شکل تابع چگالی احتمال (probability density function) قله ای تر و دارای دم پهن تر یا دنباله پهن تر(fat-tailed/ heavy-tailed) باشد میزان شاخص کشیدگی برای آن بیشتر است.

شاخص های پراکندگی
همانطور که در تصویر مشاهده می شود، با اینکه دو نمودار متفاوت از یکدیگر هستند، دارای شاخص های مرکزی یکسان هستند.
از این رو باید به بررسی شاخص های پراکندگی نیز توجه ویژه نمود.

- دامنه داده ها (Range): اختلاف کوچکترین و بزرگترین داده
- واریانس (Variance): میانگین انحراف داده ها از میانگین؛ واریانس یا وردایی عددی است که نشان میدهد چگونه یک سری داده حول مقدار میانگین پخش میشوند.
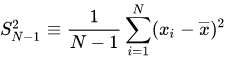
- انحراف معیار (Standard Deviation): جذر واریانس؛ نماد σ
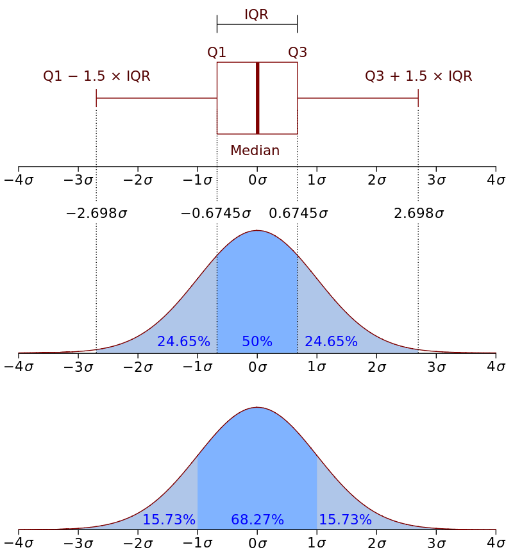
- دامنه میان چارکی(Interquartile range): اختلاف چارک اول و سوم داده ها
چارکها مقادیری هستند که دادهها را به چهار قسمت مساوی تقسیم می کنند. اگر یک رشته اعداد را از نظر تعداد به چهار قسم مساوی تقسیم کنیم، نقطه اول که ۲۵ درصد از دادهها کمتر از آن هستند چارک اول، نقطه دوم که دقیقا در سطح دادهها قرار دارد چارک دوم یا همان میانه، نقطه سوم که ۷۵ درصد از دادهها کمتر از آن هستند چارک سوم نامیده می شود.
فاصله بین چارک اول و سوم دامنه میان چارکی نامیده می شود. در محدوده دامنه میان چارکی، ۵۰ درصد داده ها قرار می گیرند.
مثال: در داده های میزان نوشیدن تعداد لیوان آب در یک سری از افراد در دو گروه که مورد سوال قرار گرفته اند، داریم:


نمودار جعبه ای (باکس پلات Box plot)
نمودار جعبه ای یا باکس پلات میانه و دامنه میان چارکی و همه چارکها را بصورت تصویری نمایش می دهد.


مثال: در مثال روبرو در مورد نتایج سوال در خصوص سن اولین ازدواج داریم.