آزمون دقیق فیشر یک آزمون اهمیت آماری در تجزیه و تحلیل جداول احتمالی است. اگرچه در عمل وقتی که نمونه اندازه کوچک باشد استفاده می شود، اما برای همه اندازه نمونه ها معتبر است. نام آن از نام مخترع آن، رونالد فیشر گرفته شده است، و یکی از کلاس های آزمون های دقیق است که به این دلیل نامیده می شود زیرا اهمیت انحراف از فرضیه صفر (به عنوان مثال، مقدارP) دقیقاً قابل محاسبه است، نه اینکه به بسیاری از آزمایشات آماری اعتماد کنید که با بزرگ شدن اندازه نمونه تا حد بی نهایت دقیق شود.
گفته می شود که فیشر به دنبال اظهار نظری از موریل بریستول، که ادعا می کند قادر به تشخیص اینکه چای یا شیر ابتدا به فنجان خود اضافه شده است، آزمایش را انجام داده است. او ادعای خود را در آزمایش “چای مزه زن” آزمایش کرد.
او به زنی در یک مهمانی عصرانه، یک فنجان چای تعارف میکند (در انگلستان عمدتاً چای را با شیر مخلوط کرده و مینوشند). زن از او میپرسد که آیا او ابتدا شیر را در فنجان ریخته و سپس چای را با آن مخلوط کرده و یا ابتدا چای را ریخته و سپس شیر را با آن مخلوط کرده است؟ فیشر از این سؤال تعجب میکند و میگوید مگر فرقی هم میکند؛ وقتی چای و شیر باهم مخلوط شوند ممکن نیست تفاوتشان در مزه مشخص شود.
زن در مقابل ادعا میکند او قادر است تفاوت فنجان چایی که ابتدا شیر در آن ریخته شده را با آنکه ابتدا در آن چای ریخته شده، تشخیص دهد. چگونه بفهمیم ادعای زن درست است؟ آیا او واقعاً استعدادی در شناسایی تفاوت این دو حالت دارد؟
پاسخ فیشر برای آزمایش ادعای زن آن است که جلوی او هشت فنجان قرار دهیم. چهار فنجان مخلوط شیر و چای که ابتدا شیر در آن ریخته شده و بعد چای و چهار فنجان دیگر که ابتدا چای و سپس شیر در آن ریخته شده است. این هشت فنجان را در یک سینی بهصورت تصادفی بچینیم.
توجه کنید که این هشت فنجان باید تا حد ممکن از بقیه نظرها مانند دمای فنجان، میزان شیرین بودن و غیره یکسان باشند و تنها در ترتیب ریختن چای و شیر باهم تفاوت کنند. در گام بعد زن باید بگوید که هر فنجان به کدام حالت تعلق دارد؟
اما چرا هشت فنجان؟ فیشر محاسبه کرده بود که ۷۰ حالت مختلف برای چینش این هشت فنجان در کنار یکدیگر وجود دارد
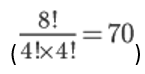
اگر آن زن دارای استعدادی نباشد، مجبور است شانسی حدس بزند که در سینی که جلوی او گذاشته شده هر فنجان به کدام حالت تعلق دارد. بهاینترتیب او به ۷۰ روش مختلف میتواند ترکیب فنجانها را حدس بزند ولی فقط یکی از این ۷۰ حالت مختلف ترکیب درست است.
یعنی اگر او بخواهد ترکیب فنجانها را صرفاً با حدس زدن تشخیص دهد، با احتمال ۱ به ۷۰ (در حدود ۱٫۴ درصد) شانس موفقیت دارد. در علم آمار به این احتمال، مقدار p و یا p-value گفته میشود. این مقدار نشان میدهد چه میزان احتمال دارد نتایج بهدستآمده، صرفاً تحت یک فرآیند تصادفی تولید شده باشد.

چون تحت شرایط بالا درست حدس زدن همه فنجانها مقدار p بسیار کوچکی دارد (معادل ۱٫۴ درصد)، فیشر نتیجه گرفت اگر آن زن همه فنجانها را درست تشخیص دهد، میتوان گفت ادعای زن درست است. پرسشی که پیش میآید این است که مقدار p باید با چه معیاری مقایسه شود؟ درواقع به چه احتمالی کوچک گفته میشود؟
فیشر این مقدار را ۵ درصد پیشنهاد کرد که امروزه یک معیار پذیرفتهشده است. به این مقدار حاشیه خطا گفته میشود. اگر حاشیه خطا ۵ درصد باشد، مفهومش این است که شما با احتمال ۹۵ درصد میتوانید مطمئن باشید که نتایج بهدستآمده بر اساس تصادف حاصل نشده است.
اگر در این مثال، فرد تنها یک اشتباه داشته باشد، مقدار p نزدیک ۲۴ درصد میشود که از حاشیه خطای ۵ درصد بزرگتر است. بهاینترتیب نمیتوان گفت این فرد با کسی که صرفاً بر اساس تصادف حدس میزند، به لحاظ آماری تفاوت معنیداری دارد. بهعبارتدیگر نمیتوانیم نتیجه بگیریم این فرد دارای استعداد ویژهای است و ادعای او را رد میکنیم. جالب است بدانید این داستان در عمل اتفاق افتاد و آن زن توانست همه فنجانها را درست تشخیص دهد.
در حالت سختگیرانهتر حاشیه خطا را ۱ درصد در نظر میگیرند. در حالت سختگیرانه با آزمایش بالا نمیتوان ادعای زن را سنجید، چراکه اگر همه فنجانها را هم درست تشخیص دهد، همچنان مقدار p بالاتر از ۱ درصد است. در این حالت باید تعداد فنجانها را افزایش داد تا بتوان ادعای او را با ۱ درصد خطا سنجش کرد. شاید پیشنهاد شود بهتر است تعداد فنجانها را آنقدر زیاد کنیم تا میزان خطا به صفر نزدیک شود. به نظر شما این پیشنهاد چه مشکل دیگری در ارزیابی ادعای زن ایجاد میکند؟
عملا در این تست دیده می شود که زن تعداد قابل قبولی از پاسخ ها را درست جواب داد (80% موارد) اما زمانی که تست کای-دو را اجرا می نماییم خواهیم دید که همه خانه های جدول expected value کوچکتر از 5 را دارند و در صورتیکه در نرم افزار این حالت برا بررسی نماییم در پایین جدول اشاره خواهد شد که 100% اعداد expected value کمتر از 5 را دارند و آزمون استقلال برقرار نخواهد شد.
بنابر این فیشر آزمون این قاعده را خواهد گذاشت که expected value ها باید کمتر از 20% باشد و آماره دیگری را طراحی نموده است و P-Value را با آن حساب می نماید.
بنابراین در حالت هایی که expected value بیشتر از 20% است باید از روش آزمون دقیق فیشر استفاده نماییم.




