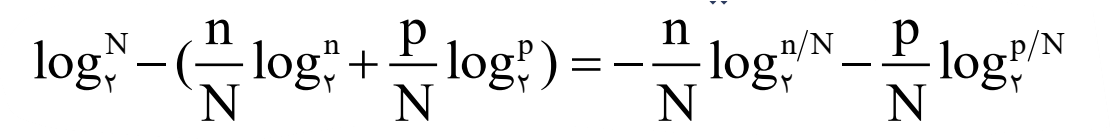نحوه آموزش درخت تصمیم
جهت توسعه درخت تصمیم باید به سوالات زیر پاسخ داد:
- کدام ویژگی برای انشعاب انتخاب شود؟
- حدود آستانه ای برای انشعاب هر ویژگی چه مقادیری باشد؟
- تعداد انشعاب ها تا کجا ادامه پیدا کند؟
آموزش درخت تصمیم در راستای کاهش ناخالصی در داده ها انجام می شود. بنابراین در اولین قدم بایستی معیار و شاخصی برای اندازه گیری میزان ناخالصی در نظر گرفت. این معیار در ادبیات آمار و نظریه اطلاع توسط شاخص های متنوعی محاسبه شده و با انشعاب روی سطوح مختلفی از ویژگی های ورودی مدل سعی در کاهش آن میکند تا شرایط توقف الگوریتم احراز گردد.
گام اول: انتخاب معیار اندازه گیری ناخالصی
نحوه انشعاب بایستی به نحوی انجام شود تا با کمترین تعداد سوال(انشعاب) به هدف اصلی یعنی کاهش ناخالصی برسد.
یک بازی فرضی را در نظر بگیرید که شما بایستی یک عدد انتخاب شده در بازه 1 تا 1024 را با کمترین تعداد سوال حدس بزنید. چه نوع سوالاتی می تواند به شما کمک کند تا در این بازی بهترین امتیاز را کسب کنید؟

اگر به همین ترتیب ادامه دهید با جمعا 10 سؤال می توانید عدد مورد نظر را بیابید. به عبارت دیگر شما به 10 بیت اطلاع نیاز دارید که از فرمول
زیر به دست می آید:
log2 𝑁 = log2 1024 = 10
نظریه اطلاع:
وقتی شما یک مجموعه N عضوی را به دو مجموعه n و p عضوی تقسیم می کنید میانگین اطلاعی که همچنان مورد نیاز می باشد برابر است با:
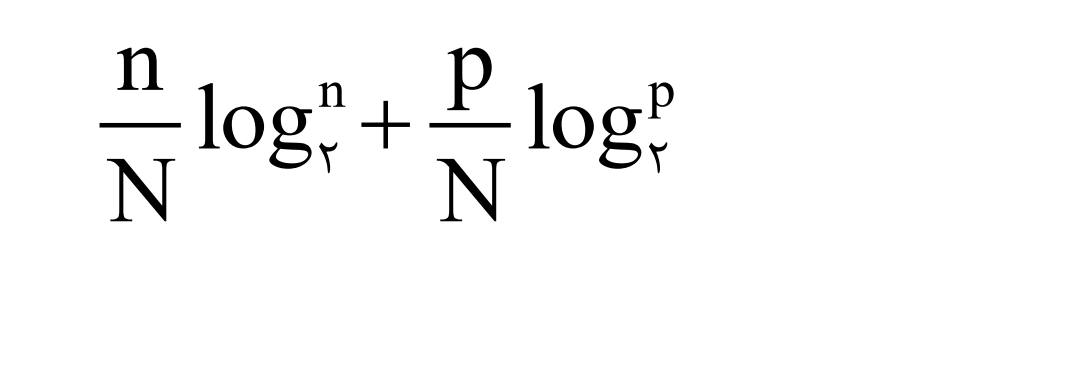
بنابراین میانگین اطلاعی که به وسیله یک سؤال فراهم مي شود برابر است با:
شاخص بی نظمی آنتروپی (Entropy)
بر اساس نظریه اطلاع، اگر رده بندي اعضاي يك مجموعه به k رده مورد نظر باشد و pk احتمال تعلق اعضا به رده kام باشد ، مقدار اطلاع مورد انتظاري كه نياز است تا اعضا به رده درست تعلق گيرند آنتروپي (شاخص بی نظمی) ناميده مي شود كه از فرمول زير محاسبه مي شود:

بیشترین میزان بی نظمی هنگامی می باشد که احتمال تعلق به تمامی رده ها، برابر است. در تصویر، نمودار میزان آنتروپی در توزیع دو جمله ای نشان داده شده است.
شاخص بی نظمی آنتروپی (Entropy)
در صورتی که مجموعه داده بر اساس انشعاب روی سطوح یک ویژگی، به دو یا چند زیرمجموعه تفکیک گردد، میزان آنتروپی حاصل از انشعاب، میانگین وزنی از آنتروپی زیرمجموعه های ایجاد شده می باشد؛ به طوری که مقدار وزن برابر با نسبت فراوانی هر زیرمجموعه به تعداد کل مجموعه اولیه می باشد.
شاخص بهره اطلاعاتی (Information Gain)
به میزان کاهش ناخالصی که بر اساس یک انشعاب ایجاد می شود، میزان بهره اطلاعاتی گفته می شود.
بطور مثال اگر مجموعه داده اولیه T را مجموعه تمام روزهای یک سال در نظر بگیریم که دارای توزیع دو جمله ای از روزهای بازی یا عدم بازی گلف باشد و (T , X) را انشعاب مجموعه T روی ویژگی شرایط آب و هوا (آفتابی/ابری/بارانی) در نظر بگیریم، میزان بهره اطلاعاتی ناشی از انشعاب شرایط آب و هوایی بر اساس رابطه زیر بدست می آید.
الگوریتم درخت تصمیم ID3 از شاخص بهره اطلاعاتی برای انتخاب بهترین انشعاب استفاده میکنند. برای این منظور در انشعاب هر گره، میزان بهره اطلاعاتی برای تمام ویژگی ها در تمام حالات امکانپذیر محاسبه می شود و در نهایت ویژگی منتخب و سطوح تفکیک آن بر اساس بیشترین میزان بهره اطلاعاتی بدست می آید.

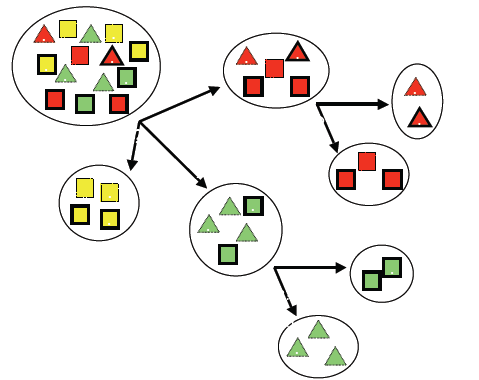
مثال:
فیلد هدف: کلاس های مربع و مثلث
ویژگی های ورودی: رنگ: قرمز/سبز/زرد
نقطه: بله /خیر
خط: بله /خیر
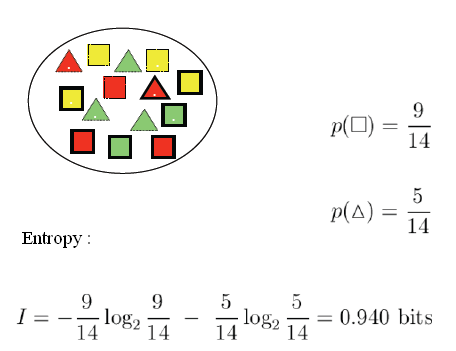
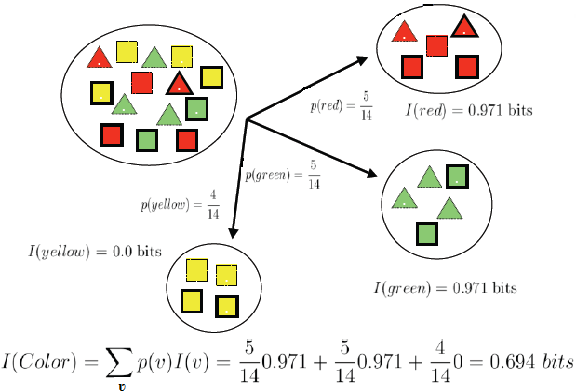


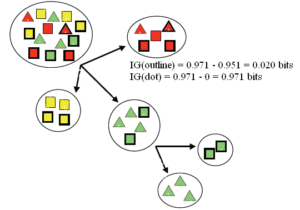
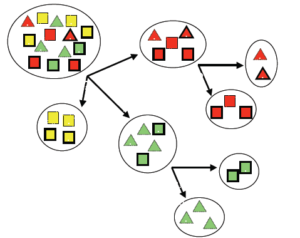
شاخص نسبت بهره (Gain Ratio Index)
اندازه بهره اطلاعاتی در انشعاب هایی که تعداد رده های بیشتری دارند بطور کاذب افزایش پیدا می کند و شانس انتخاب ویژگی هایی که دارای تعداد رده بیشتری هستند را نسبت به سایر ویژگی ها بیشتر میکند.
برای جلوگیری از این مشکل محاسباتی، کافیست نرمال سازی میزان بهره اطلاعاتی هر ویژگی را با تقسیم بر مقدار آنتروپی توزیع انشعاب محاسبه کنیم. شاخص نسبت بهره در الگوریتم های توسعه یافته بر مبنای ID3 مانند الگوریتم های C4.5 و C5.0 جایگزین شاخص بهره اطلاعاتی شده است.

شاخص ناخالصی جینی (Gini Impurity Index):
این شاخص در الگوریتم CART برای جداسازی و انشعاب مورد استفاده قرار می گیرد. فرض کنید مجموعه داده در گره T دارای K رده مختلف از کلاس هدف می باشد. شاخص ناخالصی جینی بر اساس رابطه زیر بدست می آید:

محاسبه مقدار شاخص جینی برای هر انشعاب و همچنین میزان بهره حاصل از کاهش میزان شاخص جینی مشابه توضیحات قبلی می باشد.

مقدار بیشینه شاخص ناخالصی جینی در حالتی که احتمال دو رده کلاس هدف برابر باشد، مقدار 0.5 خواهد بود.
مشابه روال قبل در انشعاب هر گره، میزان شاخص جینی برای تمام ویژگی ها در تمام حالات امکانپذیر محاسبه میشود و در نهایت ویژگی منتخب و سطوح تفکیک آن براساس کمترین میزان شاخص جینی به دست می آید.

شاخص کاهش انحراف معیار (Standard Deviation Reduction)
در الگوریتم هایی مانند، CART کاهش انحراف معیار در مسائلی که فیلد هدف دارای توزیع کمی باشد مورد استفاده قرار می گیرد. در حالت Regression Tree مقدار میانگین یا میانه در هر گره محاسبه شده و براساس رابطه شاخص پراکندگی (واریانس /انحراف معیار /…) نسبت به معیار مرکزی آن گره میزان ناخالصی آن گره و انشعاب های آن محاسبه می شود.
محاسبه مقدار شاخص پراکندگی برای هر انشعاب و همچنین میزان بهره حاصل از کاهش میزان شاخص پراکندگی مشابه توضیحات قبلی می باشد.
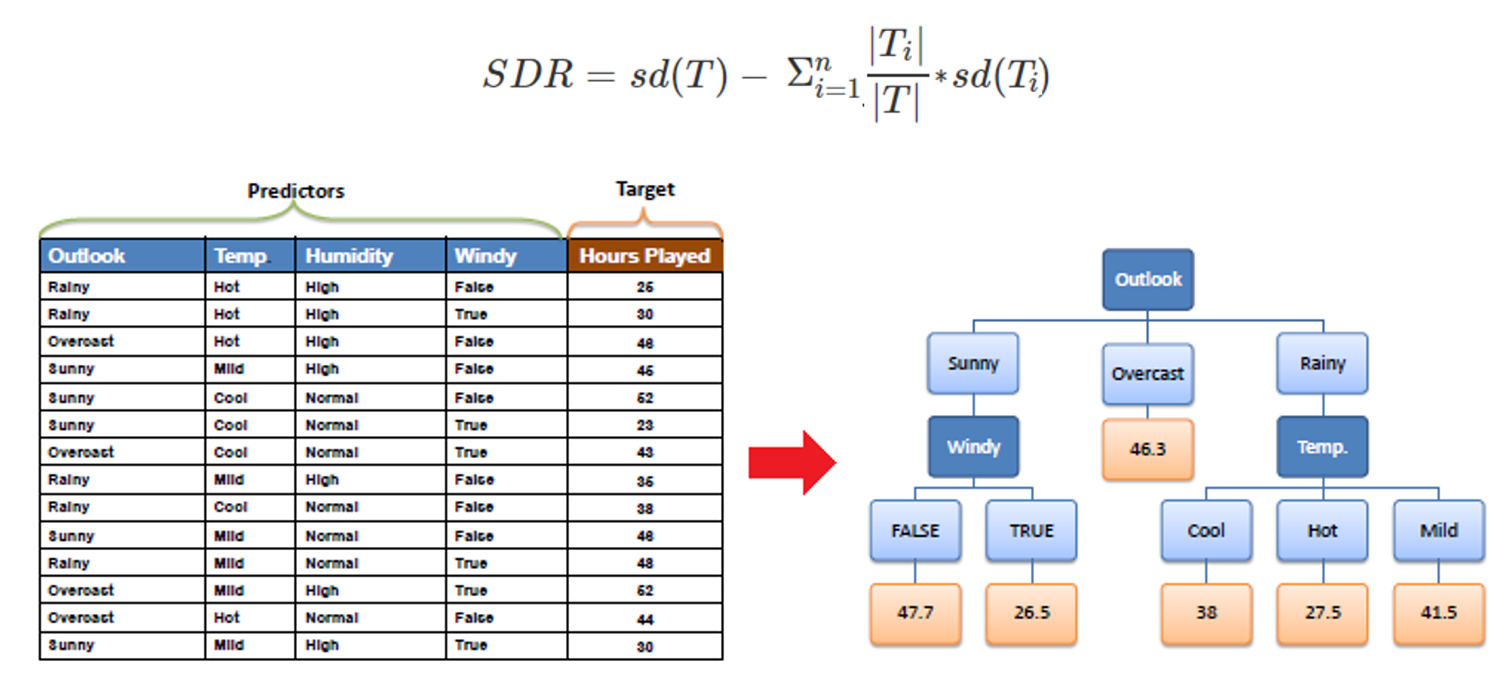
شاخص اختلاف کای-دو (Chi-Square Index)
در الگوریتم درخت تصمیم CHAID از شاخص آماری کای –دو برای محاسبه شاخص ناخالصی استفاده شده است. با توجه به رابطه کای – دو ایده اصلی در بررسی اختلاف بین توزیع واقعی و توزیع قابل انتظار می باشد. در این الگوریتم توزیع قابل انتظار، شرایط کاملا برابر کلاس های فیلد هدف در هر گره می باشد؛ به همین دلیل هرچه مقدار کای – دو بزرگتر باشد نشان دهنده خلوص بیشتر در گره میباشد.
الگوریتم CHAID در حالت درخت رگرسیونی برای پیش بینی مقادیر کمی، با محاسبه آماره F و تعیین بزرگترین مقدار آن به عنوان بهترین انشعاب، آموزش درخت تصمیم را انجام می دهد.
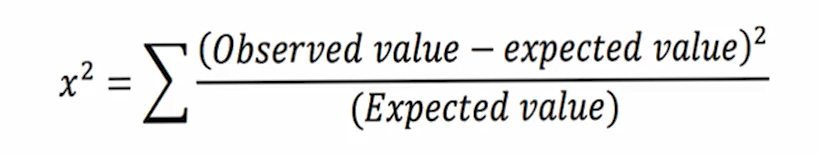
گام دوم: انتخاب بهترین انشعاب برای هر ویژگی
پس از انتخاب معیار مناسب برای اندازه گیری میزان ناخالصی، برای ایجاد انشعاب روی هر ویژگی بسته به توزیع کمی یا کیفی ویژگی مربوطه از روش های زیر استفاده می شود.
ویژگی های کیفی
- درصورتیکه ویژگی باینری باشد، انشعاب دو تایی ایجاد شده و معیار ناخالصی برای آن محاسبه و ثبت می گردد.
- در صورتی که ویژگی اسمی دارای k مقدار باشد، تمام حالت های ممکن برای انشعاب دوتایی، 3تایی، … و -kتایی ایجاد و معیار ناخالصی برای همه آنها محاسبه شده و انشعاب دارای کمترین مقدار ناخالصی برای آن ویژگی انتخاب می شود.
- در صورتی که ویژگی ترتیبی و دارای k مقدار باشد، تمام حالت ها ممکن برای انشعاب دوتایی، 3تایی، … و -k تایی با شرط حفظ همسایگی مقادیر ویژگی ایجاد و معیار ناخالصی برای همه آنها محاسبه شده و انشعاب دارای کمترین مقدار ناخالصی برآن آن ویژگی انتخاب می شود.
- جهت تعیین تعداد انشعاب ویژگی های کمی و مقادیر آستانه ای آن، مراحل زیر انجام می شود:
- کلیه مقادیر یکتای ویژگی کمی مورد نظر، از کوچک به بزرگ مرتب می شوند.
- حد وسط مقادیر به عنوان نقاط آستانه ای اولیه انتخاب شده و گسسته سازی بر اساس بازه های ایجاد شده انجام می شود.
- مشابه داده های ترتیبی، تمامی انشعاب های ممکن انجام و معیار ناخالصی برای آنها محاسبه شده و انشعاب دارای کمترین میزان ناخالصی به عنوان بهترین انشعاب برای آن ویژگی انتخاب میشود.
گام سوم: انتخاب بهترین ویژگی برای هر گره
در هریک از گره های تصمیم گیری، پس از بررسی تمامی حالات ممکن انشعاب برای هر یک از ویژگی ها و انتخاب بهترین حالت برای آنها، الگوریتم درخت تصمیم به مقایسه میزان ناخالصی ایجاد شده بین تمام ویژگی ها پرداخته و بهترین ویژگی برای ایجاد کمترین ناخالصی را برای انشعاب در نظر میگیرد.
بعد از ایجاد انشعاب، هر یک از گره های ایجاد شده جدید مستقلا به عنوان یک گره تصمیم در نظر گرفته شده و کلیه مراحل گفته شده برای هر یک از آنها تکرار می شود تا بر اساس قوانین توقف الگوریتم از رشد بیشتر درخت جلوگیری شود.
گام چهارم:هرس کردن درخت تصمیم
مرحله مهم دیگر در ساخت درخت تصمیم استفاده از روش های هرس کردن درخت به منظور جلوگیری از بیش برازش شدن مدل میباشد. در نتیجه با حذف قوانین ضعیف و ساده کردن مدل درخت تصمیم، در کنار افزایش قدرت تعمیم پذیری، میزان تفسیرپذیری مدل نیز افزایش می یابد.
تکنیک های هرس درخت با دو رویکرد انجام میپذیرد:

روش پیش هرس کردن درخت تصمیم (Pre-Pruning)
بطور معمول از طریق تنظیم قوانین توقف زیر میتوان از توسعه درخت تصمیم جلوگیری کرد:
- تعیین عمق درخت تصمیم
با تعیین عمق درخت تصمیم می توان تعداد انشعاب ها را کنترل کرد. بدین ترتیب در صورتی که انشعاب یک گره، از حداکثر عمق مشخص شده بیشتر گردد، اجازه انشعاب وجود نداشته و آن گره به عنوان گره پایانی یا برگ در نظر گرفته می شود.
- تعیین حداقل رکورد برای انشعاب
با تعیین تعداد حداقل رکورد برای انشعاب، در صورتی که تعداد رکوردهای یک گره از میزان مشخص شده کمتر باشد، اجازه انشعاب صادر نشده و آن گره به عنوان گره پایانی در نظر گرفته میشود.
- تعیین حداقل رکورد برای گره پایانی
با تعیین تعداد حداقل رکورد برای گره پایانی، در صورتی که انشعاب گره والد، منجر به ایجاد گره هایی با کمتر از تعداد رکورد تعیین شده شود، اجازه انشعاب صادر نشده و گره والد به عنوان گره پایانی یا برگ در نظر گرفته می شود.
روش پس هرس کردن درخت تصمیم (Post-Pruning)
در این رویکرد، درخت تصمیم اولیه بدون محدودیت ساخته می شود. سپس بر اساس اندازه گیری میزان هزینه توسعه آن، در خصوص حذف و هرس کردن بخش هایی از درخت تصمیم گیری میشود.
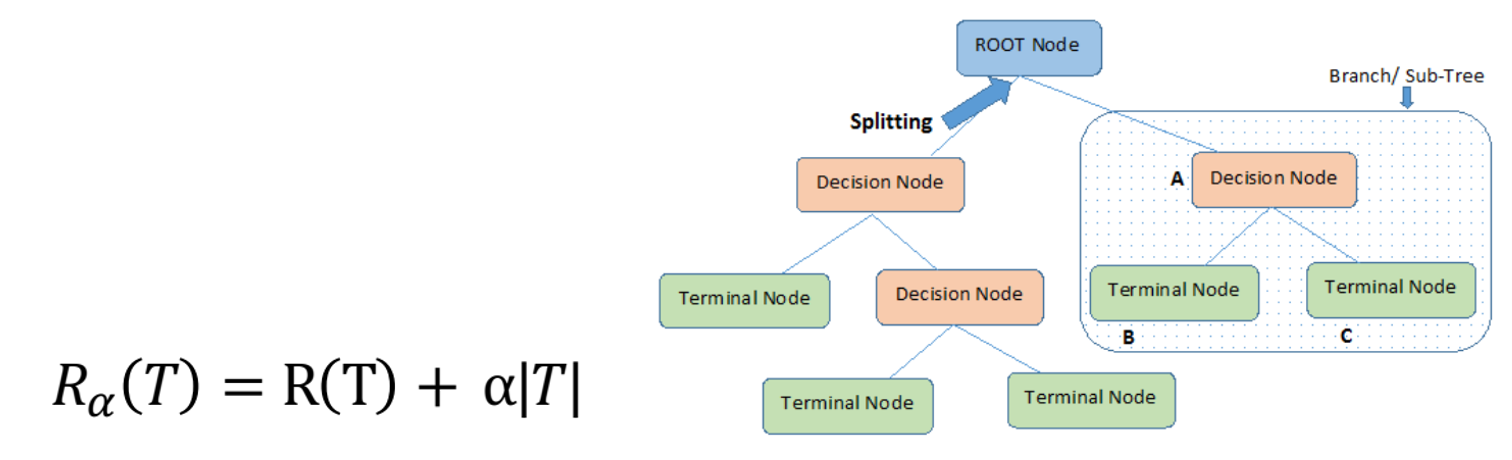
(T)R: مجموع خطای آموزش در گره های پایانی (برگ ها)
|T|: تعداد کل گره های پایانی (برگ ها)
α : میزان شدت هرس