الگوریتم K-Means یکی از پرکاربردترین و محبوب ترین الگوریتم های خوشه بندی افرازی می باشد. در این الگوریتم، با در نظر گرفتن تعداد خوشه به اندازه K، الگوریتم سعی در تقسیم بندی داده ها در k خوشه می کند بطوریکه تمامی رکوردهای درون یک خوشه به مرکز آن خوشه نزدیکتر از مراکز خوشه های مجاور باشند.
گام های پیاده سازی الگوریتم K-Means
گام اول: انتخاب K رکورد از مجموعه داده ها به عنوان مراکز خوشه اولیه
گام دوم: برچسب گذاری تمام رکوردها بر مبنای فاصله از مراکز خوشه اولیه
گام سوم: به روز رسانی مراکز خوشه
گام چهارم: تکرار گام های دوم و سوم تا رسیدن به شرایط توقف
● گام اول: انتخاب K رکورد از مجموعه داده ها به عنوان مراکز خوشه اولیه
معمولا مراکز خوشه اولیه به صورت تصادفی از بین داده ها انتخاب می شود. و این موضوع می تواند بعضا منجر به نتایج متفاوتی در شناسایی الگوها گردد. در واقع الگوریتم K-Means به نقاط اولیه حساس می باشد.
یکی از روش های رایج برای کنترل این مشکل، اجرای چند باره الگوریتم است. همچنین استفاده از الگوریتم خوشه بندی سلسله مراتبی و انتخاب نمونه ای از خوشه های بدست آمده در آن می تواند گزینه دیگر باشد.

● گام دوم: برچسب گذاری تمام رکوردها بر مبنای فاصله از مراکز خوشه اولیه
با محاسبه معیار فاصله (به طور مثال فاصله اقلیدسی) تمامی رکوردها با هر یک از مراکز خوشه، برچسب خوشه ای که دارای کمترین فاصله باشد، به رکورد مورد نظر الحاق می گردد.

● گام سوم: به روز رسانی مراکز خوشه
با میانگین گیری از مقادیر هر یک از ویژگی های ورودی به تفکیک خوشه ها، مراکز خوشه جدید محاسبه شده و جایگزین مراکز قبلی می شود.
وجود داده های پرت و نویزی در محاسبه میانگین، خطا ایجاد می کند؛ بنابراین یکی از راه های معرفی شده استفاده از میانه به جای میانگین هست که در الگوریتم K-Medoids استفاده می شود.

● گام چهارم: تکرار گام های دوم و سوم تا رسیدن به شرایط توقف

فرضیات و محدودیت های الگوریتم K-Means
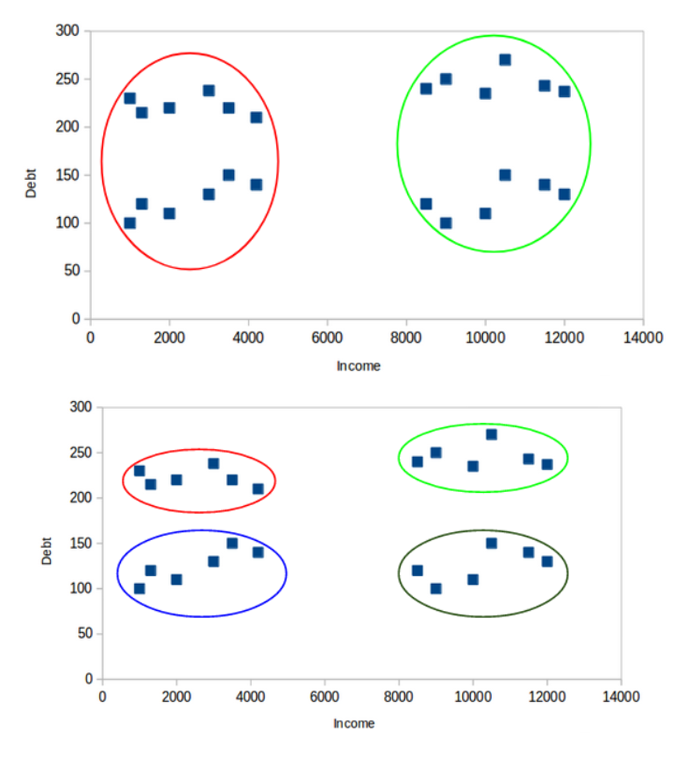
● فرض هم اندازه بودن خوشه ها
با توجه به اینکه الگوریتم K-Means به دنبال کمینه کردن مقدار SSE می باشد، بنابراین تمایل به شکستن خوشه های بزرگ و ایجاد خوشه های هم اندازه دارد. با افزایش تعداد K، میتوان این مشکل را برطرف کرد.
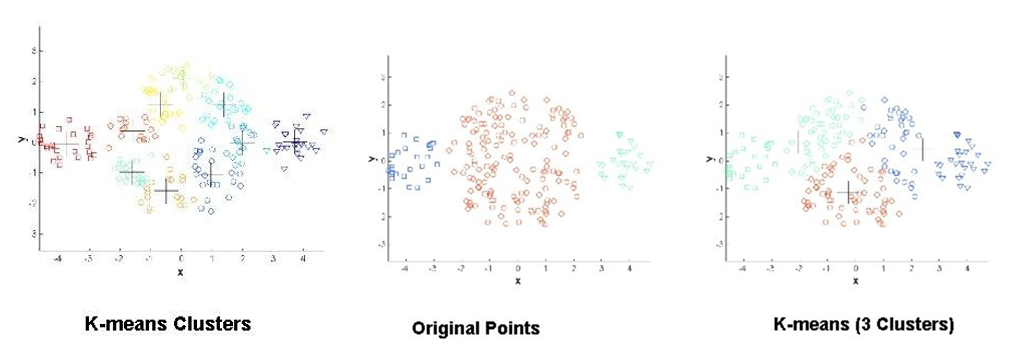
فرض یکسان بودن تراکم خوشه ها
با توجه به اینکه الگوریتم K-Means به دنبال خوشه هایی با فاصله های کمتر (شبیه تر) به هم می باشد، تراکم داده ها تاثیری بر محاسبات آن ندارد و قادر به شناسایی همچین الگوهایی نیست. با افزایش تعداد K، میتوان این مشکل را برطرف کرد.

فرض کروی بودن ساختار خوشه ها
با توجه به اینکه الگوریتم K-Means فرض میکند واریانس هر یک از ویژگی ها به صورت کروی است، تنها قادر به شناسایی الگوی خوشه های کروی می باشد و نمی تواند الگوهای غیرکروی را به درستی خوشه بندی کند. با افزایش تعداد K، میتوان این مشکل را برطرف کرد.

کمی بودن ویژگی های ورودی
با توجه به اینکه الگوریتم K-Means با استفاده از میانگین گیری مراکز خوشه را محاسبه می کند، بنابراین این الگوریتم برای ویژگی های ورودی کمی قابل استفاده است. اما با توجه به اینکه در مسائل واقعی عموما ترکیبی از داده های کمی و کیفی وجود دارد، راهکار مورد استفاده برای حل این مشکل، استفاده از کد گذاری عددی برای داده های کیفی است.
عموما داده های ترتیبی پس از کدگذاری به روش Label Encoding و داده های اسمی با روش One Hot Encoding به الگوریتم K-Means وارد می شود.

نکته: استفاده از روش One Hot Encoding با کد گذاری صفر و یک باعث می شود در محاسبه فاصله بین دو رکورد، یک تغییر در رده فیلد کمی به اندازه جذر 2 (به مقدار 1.41) فاصله ایجاد کند، در صورتی که یک واحد تغییر در داده های کمی به مقدار 1 واحد فاصله ایجاد کند. از این رو در برخی مواقع میتوانیم برای ایجاد تاثیر یکسان از کد گذاری 0 و استفاده کنیم.

تعیین تعداد خوشه مناسب
الگوریتم K-Means برای اجرا نیاز به معلوم بودن تعداد خوشه دارد. اما در واقعیت تعداد خوشه های مناسب یک پارامتر نامعلوم میباشد. استفاده از الگوریتم های دیگر مانند خوشه بندی سلسله مراتبی برای تعیین تعداد خوشه یکی از راهکارهای حل این مشکل هست.
اما روش رایج برای تعیین تعداد خوشه مناسب، اجرای الگوریتم به ازای تعداد خوشه های متفاوت و مقایسه مقدار کارایی آنها بر اساس شاخص های ارزیابی الگوریتم های خوشه بندی میباشد.
در اغلب مسائل، دامنه جستجوی تعداد خوشه، بر اساس تجربیات پیشین در مسئله و الزامات کسب و کار به دست می آید و با مقایسه شاخص های ارزیابی آنها مانند میزان SSE، تعداد خوشه بهینه انتخاب می گردد. برای این منظور استفاده از نمودار Elbow بسیار رایج است.