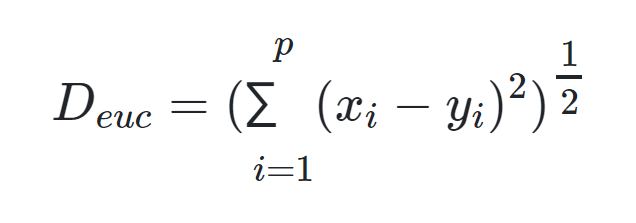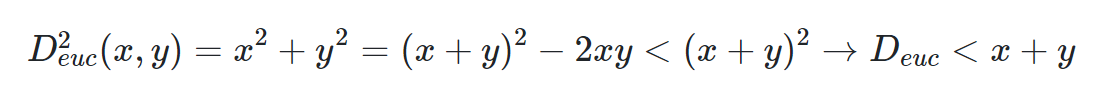همانطور که از اسم این الگوریتم مشخص است، این روش سلسله مراتبی از خوشه ها ایجاد می کند.
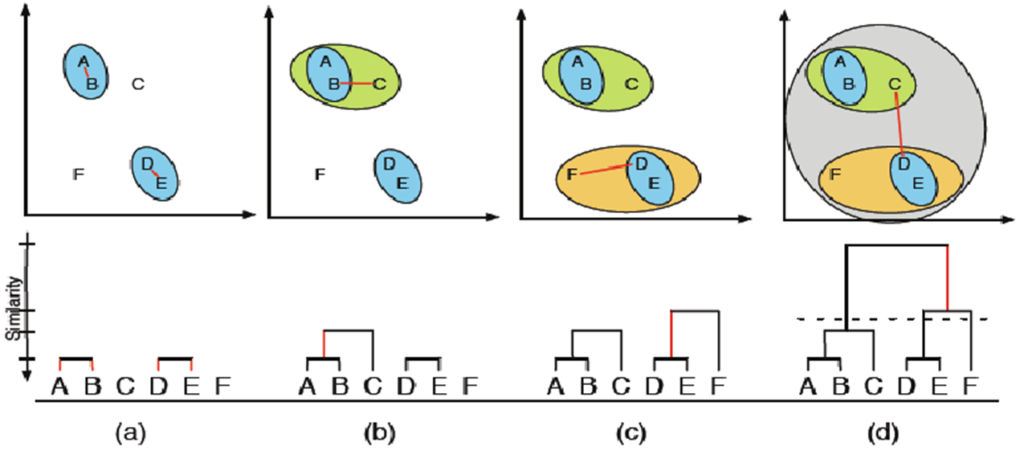
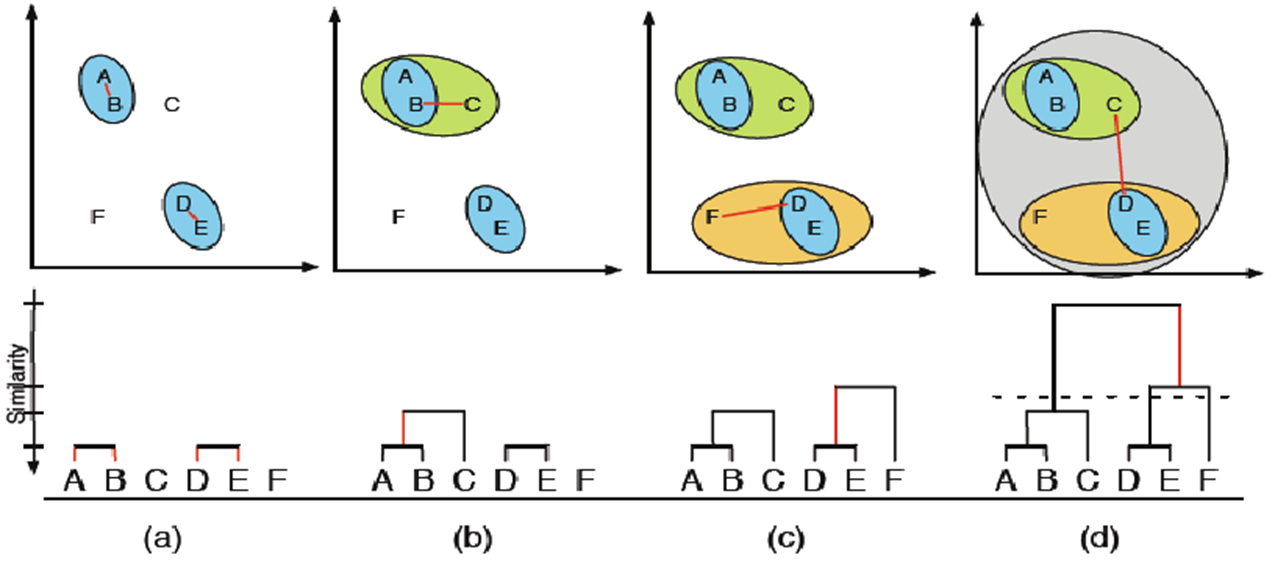
در قدم اول هریک از رکوردها را به عنوان یک خوشه در نظر می گیرد. سپس نزدیکترین رکورد ها (شبیه ترین ها) را در یک سطح بالاتر در خوشه دیگری قرار می دهد و این عمل را آنقدر ادامه می دهد تا تمام رکورد ها در یک خوشه قرار گیرند.
با این روش سلسله مراتبی از خوشه ها ایجاد می شود و با انتخاب هر سطح می توان خوشه های به دست آمده در آن لایه را استخراج کرد. (رویکرد پایین به بالا Agglomerative Approach)
در اجرای این الگوریتم به چند نکته می توان توجه نمود:
- می توان با رویکرد بالا به پایین (Top – Down) در قدم اول، همه رکوردها را در یک خوشه قرار داد و در هر قدم دورترین رکوردها (کمترین شباهت) را جدا کرده و به خوشه جدید منتقل کرد. این عمل را آنقدر ادامه داد تا تمام رکوردها به عنوان یک خوشه در نظر گرفته شوند.
- اجرای این الگوریتم نیاز به محاسبه ماتریس شباهت بین رکورد ها دارد. بنابراین با افزایش داده ها، زمان اجرای الگوریتم و نیاز به حافظه رم افزایش پیدا می کند.
- عامل تعیین کننده در پیاده سازی این الگوریتم نحوه محاسبه شباهت می باشد که دارای معیارها و رویکردهای متفاوت است.
معیارهای متفاوتی برای اندازه شباهت بین دو رکورد می توان در نظر گرفت:
فاصله اقلیدسی
با استفاده از «فاصله اقلیدسی» (Euclidean Distance) کوتاهترین فاصله بین دو نقطه بر طبق رابطه فیثاغورث، محاسبه میشود. اگر x و y دو نقطه با p مولفه باشند، فاصله اقلیدسی بین این دو به صورت زیر قابل محاسبه است:
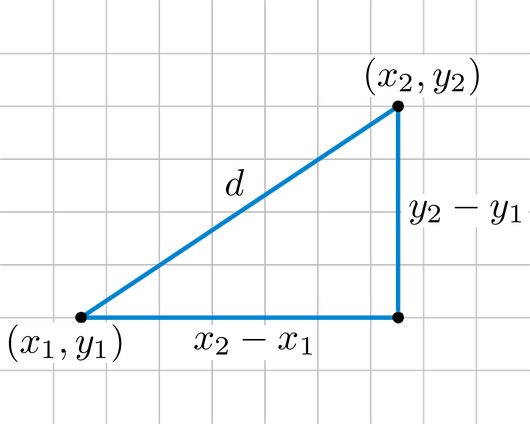
در تصویر زیر، فاصله اقلیدسی بین دو نقطه با مختصات (x1,y1)(x1,y1) با (x2,y2)(x2,y2) نشان داده شده است.
در ادامه به بررسی خصوصیات تابع فاصله برای فاصله اقلیدسی میپردازیم.
- فاصله اقلیدسی باید نامنفی باشد: مشخص است که این رابطه مقداری نامنفی دارد زیرا از مجموع مربعات تفاضلها ساخته شده است.
- وجود رابطه انعکاسی برای فاصله اقلیدسی: برای نقطههای x و y با مقدار مولفههای یکسان، فاصله اقلیدسی برابر با صفر خواهد بود. همچنین زمانی که فاصله اقلیدسی صفر باشد باید همه مربعات تفاضلها صفر باشند، در نتیجه دو نقطه بر هم منطبق هستند.
- رابطه مثلثی برای فاصله اقلیدسی: اگر دو نقطه A به مختصات (x1,y1) و نقطه B به مختصات (x2,y2) وجود داشته باشند و همچنین (x1−x2)=x;(y1−y2)=y در نظر گرفته شود، میتوان نوشت:
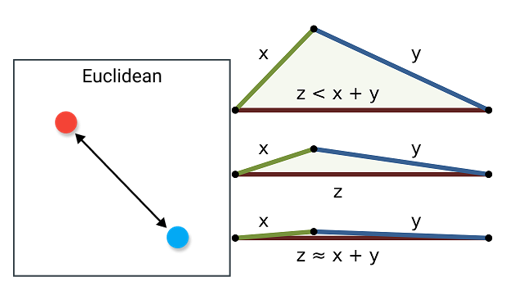
که نشان میدهد فاصله اقلیدسی در نامساوی مثلثی صدق میکند. بر طبق تصویر زیر، نیز میتوان مشاهده کرد که فاصله اقلیدسی در رابطه مثلثی صادق است.
فرض کنید دو نقطه A و B در فضای دو بعدی با مختصات (2,4) و (4,5) وجود داشته باشد. فاصله این دو نقطه بر حسب فاصله اقلیدسی برابر است با:
رایج ترین معیار فاصله که در صورت کم بودن تعداد ویژگی ها به علت سادگی و شهودی بودن آن، نتایج بسیار خوبی خواهد داشت.
- فاصله منهتن
- درک شهودی و تجسم این معیار نسبت به فاصله اقلیدسی سخت تر است ولی معمولا در داده های با ابعاد بالا عملکرد خوبی نشان می دهد.
- اگر به جای مربع فاصله بین مولفهها، از قدر مطلق فاصله بین مولفههای نقاط استفاده شود، تابع فاصله را «منهتن» (Manhattan) مینامند. این نام به علت تقاطع منظم خیابانها در محله منهتن نیویورک انتخاب شده است. البته این فاصله گاهی به نام «فاصله تاکسی» (Taxicab) یا «بلوک شهری» (City Block) نیز نامیده میشود.
- اگر x و y دو نقطه با p مولفه (P بعدی) باشند، شیوه محاسبه فاصله منهتن به صورت زیر خواهد بود:
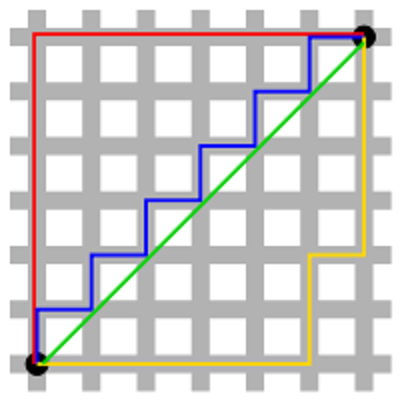
همانطور که در تصویر زیر دیده میشود، اگر محور افقی و عمودی به طولهای برابر و مساوی با ۱ تقسیم شده باشند، بین دو نقطه سیاه رنگ، مسیرهای مختلفی با فاصله منهتن یکسان وجود دارد. خطهای قرمز و آبی و زرد، مسیرهایی با فاصله منهتن ۱۲ بین این دو نقطه هستند، در حالی که خط سبز نشان دهنده فاصله اقلیدسی است که با طول برابر با کوتاهترین مسیر را (در صورت وجود) نشان میدهد.
براساس نقاط مربوط به مثال قبلی، فاصله منهتن بین دو نقطه A و B به صورت زیر محاسبه میشود:
پس از تعیین معیار اندازه گیری شباهت، انتخاب رویکرد شباهت سنجی بین خوشه ها نیز دارای اهمیت می باشد:
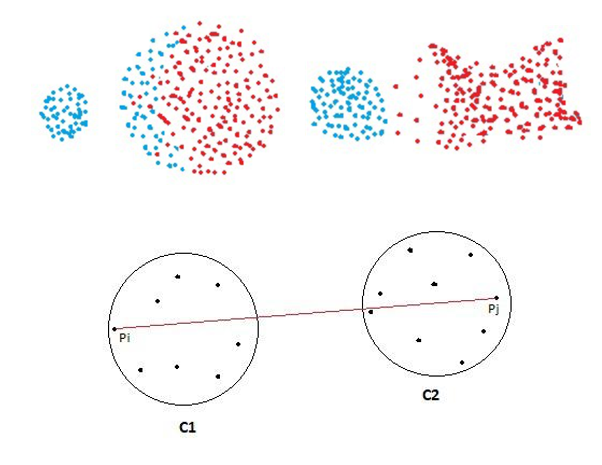
● رویکرد کمترین فاصله خوشه ها Single Linkage (Min)
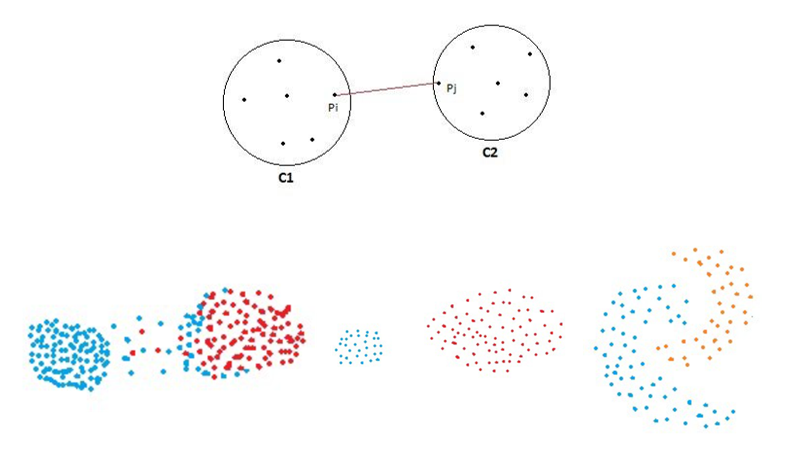
در این رویکرد فاصله بین دو خوشه، برابر با کوچکترین فاصله بین رکورد های دو خوشه می باشد.
امکان شناسایی الگوهای خوشه ای غیر بیضوی را فراهم می سازد، اما حساسیت به نویز در این روش بالاست و در صورت وجود نویز بین خوشه ها عملکرد مناسبی نخواهد داشت.
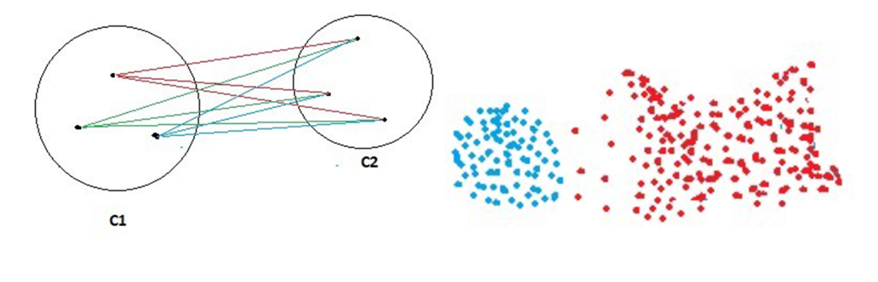
● رویکرد بیشترین فاصله خوشه ها Complete Linkage (Max)
در این رویکرد فاصله بین دو خوشه، برابر با بزرگترین فاصله بین رکورد های دو خوشه می باشد.
این رویکرد نسبت به نویزهای موجود بین خوشه ها مقاوم است و عموما سعی در تشخیص الگوهای کروی داشته و تمایل به شکستن خوشه های بزرگ دارد.
● رویکرد متوسط فاصله خوشه ها (Group Average)
در این رویکرد فاصله بین دو خوشه، برابر با متوسط فاصله بین تمام رکورد های دو خوشه می باشد.
این رویکرد نسبت به نویزهای موجود بین خوشه ها مقاوم است و عموما سعی در تشخیص الگوهای کروی دارد.
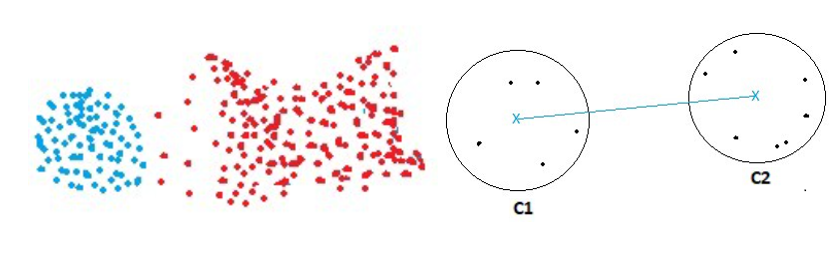
● رویکرد فاصله از مراکز خوشه (Distance From Centroids)
در این رویکرد فاصله بین دو خوشه، برابر با فاصله بین مراکز دو خوشه می باشد.
این رویکرد نسبت به نویزهای موجود بین خوشه ها مقاوم است و عموما سعی در تشخیص الگوهای کروی دارد.
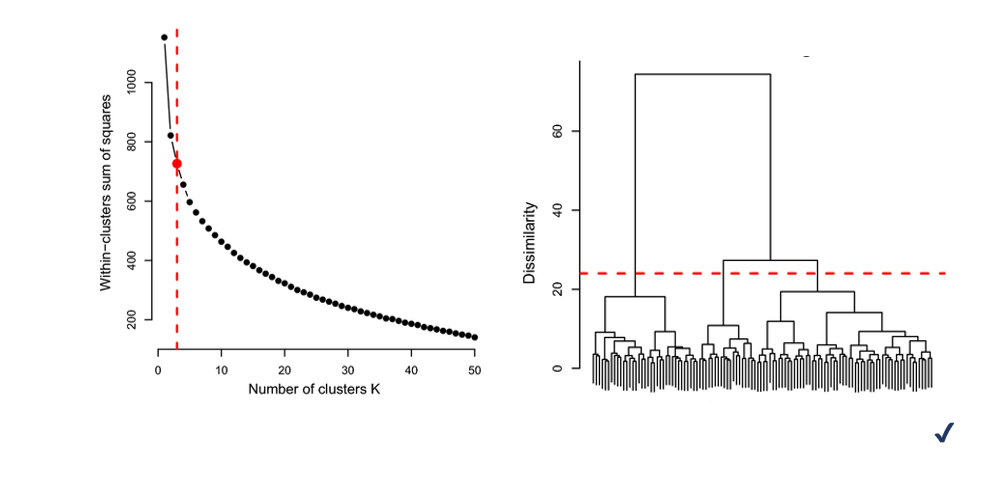
پس از اجرای الگوریتم با مقایسه شاخص های ارزیابی مجموع مربعات داخلی خوشه ها، تعداد خوشه بهینه انتخاب میگردد. برای این منظور استفاده از نمودار Elbow بسیار رایج است.