مقاله‌ی حاضر دایکه، ادامه‌ی مثال مطالعه‌ی موردی تحلیل‌های خرده‌فروشی‌مان برای راهکارهای مدیریت کمپین است. در این مورد، با دو هدف کارمان را شروع کردیم تا مدل‌ها را به‌منظور شناسایی (۱) علاقه‌مندترین مشتریان و (۲) درآمدزاترین مشتریان بسازیم.
توصیف: بخش ۳
تحلیل وابستگی: بخش ۴
دسته‌بندی: بخش‌های ۵، ۶، ۷ و ۸
برآورد: بخش ۹
ازطریق الگوریتم‌های دسته‌بندی داده‌کاوی به هدف اول رسیدیم و رفتیم سراغ هدف بعدی. در این بخش، بحث را با مدل‌های رگرسیون و برآورد ادامه می‌دهیم.
قطارها و مدل‌های رگرسیون
گالیلئو گالیه، ایساک نیوتون و آلبرت انیشتین همگی طرفدار جبرگرایی بودند. گزاره‌ی «خدا تاس‌بازی نمی‌کند»، شیوه‌ی انیشتین در بیان این امر بود که زندگی شما، زندگی من و هر چیز دیگری در این جهان مسیرهای مقدری را دنبال می‌کنند. وقتی بچه بودم، اولین درسم در جبرگرایی، سفرکردن ازطریق خطوط راه آهن هند به بخش‌های مختلف کشور طی تعطیلات تابستانی بود. همه‌ی واگن‌های مسافر متصل‌شده به‌واسطه‌ی نیروی محرکه‌ی موتور خط آهن رانده می‌شدند. دنبال‌کردن مسیر معین ریل راه آهن برای قطار مقدر شده بود. این فلسفه‌ی اساسی مدل‌های رگرسیون هم هست.
همبستگی، علیت و انطباق (تصادف) – قطارها و مدل‌های رگرسیون
ایده‌ی اصلی مدل‌های رگرسیون، یافتن نیروهای محرکه‌ای مثل موتور قطار و تعیین مسیر ریل راه آهن است. به‌طور کلی، یکی از مفاهیم کلیدی مدل‌های رگرسیون یا علم، ایجاد تمایز بین همبستگی و علیت است. بیایید سعی کنیم این موضوع را ازطریق مثال قطارها، که در آن همه‌ی واگن‌های متصل‌شده توسط موتور رانده می‌شوند را بفهمیم. جهت حرکت کلیه‌ی این واگن‌ها همبسته است. هرچند، موتور علت این جهت است. اگر چندتایی از واگن‌ها را از سایر واگن‌ها جدا کنید، قطار هنوز در همان جهت حرکت می‌کند؛ هرچند، حذف موتور قطار را کاملاً متوقف خواهد کرد.
در تصویر زیر، می‌توانید همبستگی بین متغیرهای «تعداد نوزادانی که اسمشان آوا هست» و «شاخص قیمت مسکن» را ببینید. این به احتمال زیاد نوعی همبستگی یا انطباق کاذب است. یک جورایی شبیه کسی است که خودرویی را در جاده‌ای به‌موازات چند کیلومتری قطار می‌راند. خودرو و قطار همبستگی کاملی برای این سفر خواهند داشت، اما اگر سعی کنید مکان قطار را برمبنای موقعیت این خودرو بیابید، باید بگوییم موفق باشید!
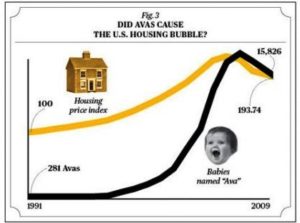
منبع: businessweek.com
مثال مطالعه‌ی موردی – مدل رگرسیون
اجازه دهید به مثال مطالعه‌ی موردی‌مان برگردیم و مدل رگرسیونی برای برآورد سودآوری هر مشتری برای مدیریت کمپین بسازیم. در بخش قبلی، با استفاده از متغیر دسته‌ای، یعنی دسته‌ی مکانی مشتریان (شهرهای کوچک، متوسط و بزرگ) مدل رگرسیون ساده‌ای ساختیم. این بار، متغیر پیوسته‌ی «سود تولیدشده توسط مشتریان در بخش قبلی» را بررسی می‌کنیم تا سودی که مشتریان ازطریق کمپین‌ها تولید می‌کنند را تعیین کنیم. شکل زیر، نمودار پراکندگی این دو متغیر است:
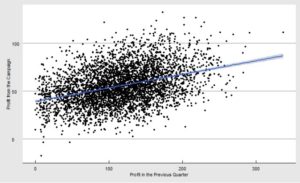
مدل رگرسیون
همبستگی معینی بین متغیرهای بالا دیده می‌شود. اگر ضرایب همبستگی یا گشتاور ضربی کارل پیرسون[1] را برای این متغیرها حساب کنیم، مقدار بسیار قابل‌توجهی به‌دست می‌آید:
رابطه‌ی بین این دو متغیر عمدتاً همبستگی است. سود در بخش قبلی قطعاً علت سودآوری حاصل از کمپین‌ها نیست. هرچند، هر دو این متغیرها تحت تأثیر عوامل رؤیت‌ناپذیری (نیروهای محرکه) مثل علاقه‌ی مشتریان به خرید از فروشگاه آنلاین و قابلیت خرج‌کردن آنها است. بنابراین، این همبستگی کاذب یا تصادفی نیست. تمیزدادن بین همبستگی و انطباق ازطریق منطقی دقیق یقیناً برای تحلیل‌گر اهمیت دارد.
حالا، بیایید مدل رگرسیون ساده‌ای بین این دو متغیر بسازیم:
معادله‌ی خطی مدل رگرسیون فوق به‌صورت زیر است:
این مدل، اختلاف ۱۳.۸ درصدی در «سود حاصل از کمپین» را توجیه می‌کند.
حالا، با افزودن متغیر دسته‌ای دفعه‌ی پیش، یعنی «دسته‌ی مکانی»، این مدل را بسط می‌دهیم. بیایید اول همان نمودار پراکندگی را با جایگذاری این متغیر دسته‌ای ترسیم کنیم.
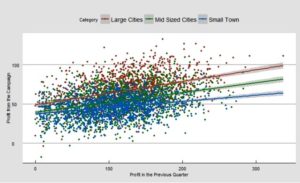
مدل رگرسیون برمبنای دسته
در تئوری، انتظار دارید سه خط «دسته‌ی مکانی» کاملاً با هم موازی باشند. هرچند، در عمل، به‌ندرت خطوط کاملا موازی (یا بدون اندرکنش) رؤیت می‌شوند. در مورد ما، این خطوط از روند مشابهی پیروی می‌کنند و اندرکنش ناچیزی دارند؛ بنابراین، می‌توانیم خیلی ساده این متغیر دسته‌ای را به مدل بالا اضافه کنیم. جدول زیر، مدل جدید پس از افزودن «دسته‌ی مکانی» را ارائه می‌دهد.
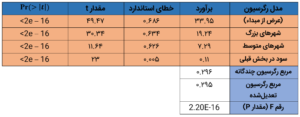
توجه کنید که مقدار مربع رگرسیون تعدیل‌شده برای این مدل ترکیبی (۰.۲۹۵) بزرگتر از متغیر پیوسته‌ی تکی (۰.۱۳۸) یا متغیر دسته‌ای (۰.۲۰۶۵) مدل‌های رگرسیون است. این فرایند توسعه‌ی مدل رگرسیون است که شمول هرگونه متغیر افزایشی در مدل مقدار مربع رگرسیون را بهبود می‌بخشد.
مخلص کلام
فلسفه‌ی جبرگرایی علم معتقد است که اگر کسی دانش کامل/ مطلقی از جهان داشته باشد، پس قادر است سرنوشت جهان را با دقت ۱۰۰ درصد یا مقدار مربع رگرسیون ۱۰۰ درصد پیش‌بینی کند. هرچند، مکانیک کوانتومی شبهه‌های خیلی جدی‌ای راجع به دیدگاه جبرگرایی جهان مطرح کرده است. طبیعت یک معما– مملو از حقه‌های تازه – است، این امر احتمالاً مهمترین منبع زیبایی ابدی محسوب می‌شود.
[1] Carl Pearson product moment
