در صورتیکه بخواهیم تاثیر دو فاکتور را بر روی یک فیلد کمی به صورت هم زمان مورد آزمون قرار دهیم از آزمون تحیلی واریانس دو طرفه استفاده می نماییم، به عنوان مثال در دیتاست Breast Cancer بخواهیم تاثیر اندازه تومور و درگیر شدن غدد لنفاوی را بر روی زمان بقا به طور هم زمان ببینیم از این آزمون استفاده می نماییم.
چرا میگوییم آنالیز واریانس دو طرفه؟
پاسخ ساده است. هنگامی که یک کمیت وابسته Dependent Variable با نام اختصاری D1 و بیش از یکFactor با نام اختصاری F>1 داشته باشیم، مطالعه ما از نوع آنالیز واریانس دو طرفه خواهد بود.

آنالیز کوواریانس چیست؟
آنالیز کوواریانس (به انگلیسی: Analyze of Covariance – ANCOVA) یا آنکوا، نوعی آنالیز و تحلیل همانند آنوا (ANOVA) میباشد و هرگاه در آنالیز واریانس بخواهیم اثر متغیرهای مداخلهگر را به روشهای آماری حذف کنیم تا نتایج با دقت بیشتری به دست آید از آنالیز کوواریانس استفاده میشود (در این روش هم از کنترل آماری استفاده میشود و هم از واریانس). بهعبارت بهتر به جای تحلیل واریانس تحلیل کوواریانس مورد استفاده قرار میگیرد.
درحقیقت آنکوا (ANCOVA) مدل ادغام شده آنوا (ANOVA) و همچنین رگرسیونی برای متغیرهای پیوسته است. تحلیل کوواریانس مناسبترین آزمون آماری برای طرح پیش آزمون و پس آزمون ۲ گروهی میباشد. و تنها عامل تهدید کننده اعتبار درونی تحلیل کوواریانس طرح پیش آزمون است.
طرح هایی که در آن ها چندین متغیر مستقل کمّی(متریک) و در ارتباط با عامل های کیفی (غیرمتریک) بکار برده می شوند، طرح های تحلیل کواریانس (ANCOVA) نامیده می شوند.
متغیر(های) مستقل کمی در این طرح متغیر کمکی و متغیر مستقل کیفی اصطلاحاً عامل نامیده می شوند. یک متغیر کمکی مؤثر در تحلیل کواریانس متغیری است که با متغیر وابسته دارای همبستگی بالایی بوده و در عین حال با سایر متغیرهای مستقل همبستگی نداشته باشد. متغیرهای کمکی پارامتری یا کمی، نوعاً در طرح های تجربی و مطالعات پیمایشی ، به منظور حذف اثرات خارجی بر متغیر وابسته و افزایش دقت اندازه گیری مورد استفاده قرار می گیرد.
کاربردهای اصلی آنالیز کواریانس
روش آنالیز کواریانس در اکثر مطالعات علوم مختلف مورد استفاده قرار می گیرد. تعدادی از این کاربردها بخصوص در پژوهش های علوم اجتماعی به شرح زیر است :
1- افزایش دقت در آزمایش هایی که در آن ها واگذاری تصادفی صورت گرفته است. وقتی کنترل مستقیم از طریق طرح آزمایش غیرعملی یا ناممکن است، آنالیز کواریانس زمینه ای را برای کنترل آماری متغیرهای مزاحم و حذف اثرات آن ها فراهم می آورد.
2- خنثی ساختن اثرات متغیرهای مزاحم در مطالعات مبتنی بر مشاهده.
3- زمانی که بخواهیم رابطه بین دو یا چند متغیر کمّی را با استفاده از نوعی تحلیل رگرسیون با متغیرهای مقوله ای بررسی کنیم.
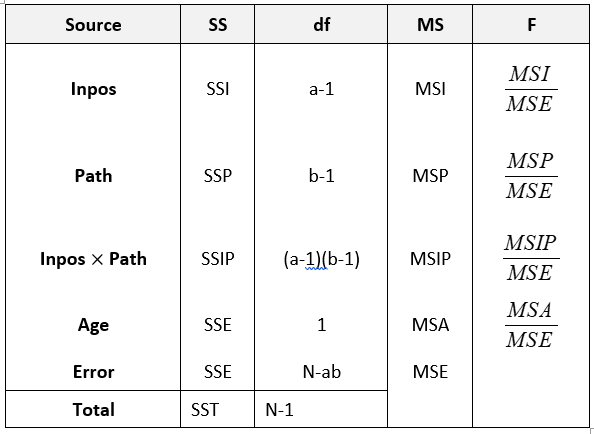
فرض کنید که در دیتاست Breast Cancer نمودار پراکندگی را برای متغییر های زمان و سن رسم می نماییم. در آنالیز کوواریانس شبیه سازی حالتی است که رگرسیونی را بین دو فیلد برقرار می نماییم و اختلاف بین عدد برازش شده و واقعی را باقیمانده (Residual) می نامند. انالیز کوواریانس میان اعداد بدست امده از باقیمانده ها انالیز واریانس را انجام می دهد.