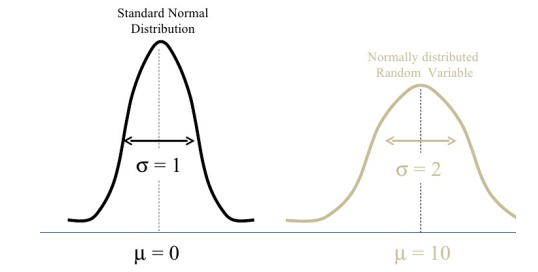
در ادامه مباحث آماری، قصد داریم انواع توزیع را معرفی نماییم:
توزیع های احتمالی
برخی از متغییر های تصادفی از تابع احتمال، با تابع چگالی خاصی پیروی می کنند که به توزیع های احتمالی استاندارد شناخته می شوند.
شناخت و درک درست از ساختار مدلی احتمالی این توزیع ها ، منجر به درک درست و دقیق از رفتار متغیر تصادفی در حل مسائل خواهد شد.
به عنوان مثال اگر دو تاس را همزمان پرتاب کنیم و این را یک آزمایش تصادفی فرض کنیم، جمع اعداد ظاهر شده همواره بین اعداد 2 تا 12 خواهد بود. در صورتی که نتایج این آزمون را نظر بگیریم فرمی که احتمال پیدا می کند برای x های مختلف را توزیع احتمال گویند.
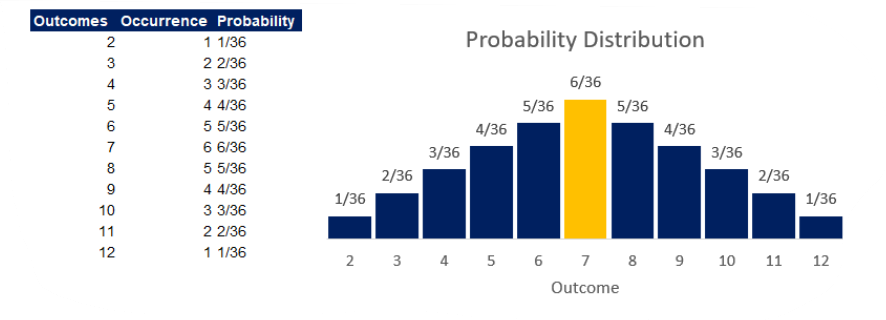
توزیع برنولی
در صورتی که آزمایشی داشته باشیم که دو برآمد داشته باشد (مثلاً شکست یا پیروزی) به آن آزمایش ازمایش برنولی گفته می شود. اگر x نمایانگر تعداد پیروزی ها باشد، x دارای توزیع برنولی با پارامتر p (احتمال پیروزی) است.
P(X=x) = px(1-p)1-x
یک سکه را به هوا پرتاب میکنیم. یا شیر میآید یا خط. اگر شیر بیاید پیروز میشویم (success) و اگر خط بیاید، میبازیم (fail). احتمالِ هر کدام هم ۵۰ درصد است. این سادهترین مثال از توزیع برنولی بود. در این توزیع که دو حالت دارد، با احتمالهای مشخصی یا برنده میشویم یا میبازیم و مجموع احتمالاتِ برد و باخت هم برابر یک میشود.
فرض کنید شخصی که دارای بیماریِ خاصی هست، سکتهی مغزی میکند و بر اساس دادههای قبلی در بیمارستان، ۲۰ درصد از افرادِ بیماری که سکتهی مغزی کردهاند، فوت میکنند (fail). پس ۸۰ درصد از آنها زنده ماندهاند (success). این هم نوعی توزیع برنولی بود. با این تفاوت که احتمالات در این مثال برابر نبودند.
اگر احتمال برنده شدن (در این مثال زنده ماندن) را برابر p در نظر بگیریم، پس p = 0.8 است و اگر احتمال شکست (در این مثال فوت کردن) را برابر q در نظر بگیریم، پس q = 0.2 است. شکل زیر نیز همین توزیع را بر روی نمودار با ۱ به معنای پیروی و ۰ به معنای شکست، مشخص میکند.
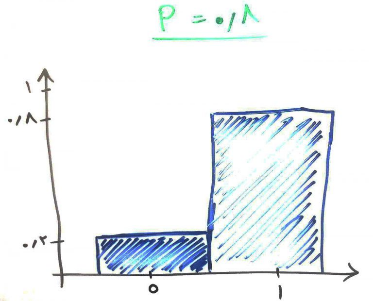
توزیع دو جمله ای
توزیع دو جمله ای بسطی از توزیع برنولی است با این تفاوت که در این توزیع یک آزمایش n بار تکرار می شود و x نمایانگر تعداد پیروزی ها سات. X دارای توزیع دوجمله ای با پارامترهای n و p (احتمال پیروزی) است.
توزیع دوجمله ای از حاصل جمع n توزیع برنولی (به شرط آن که مستقل باشند) به دست می آید. در واقع توزیع برنولی حالت خاصی از توزیع دو جمله ای محسوب می شود که در آن n برابر با یک باشد.
P(X=x) = px(1-p)n-x
فرض کنید ۱۰ بیمار سکتهی مغزی میکنند. بر اساس دادههای قبلیِ بیمارستان هم میدانیم که بیماری که سکته میکند به احتمال ۸۰ درصد زنده مانده و به احتمال ۲۰ درصد فوت میکند. حالا اگر بخواهیم بدانیم که با چه احتمالی، دقیقاً ۷ نفر از ۱۰ نفر بیماری که سکته کردهاند، زنده میمانند، بایستی از توزیع دو جملهای استفاده کنیم.
این توزیع برای پاسخگویی به همین دست سوالات به وجود آمده است. فرمولِ به دست آوردن احتمال موفقیت (success) در توزیع دو جملهای به صورت زیر است:
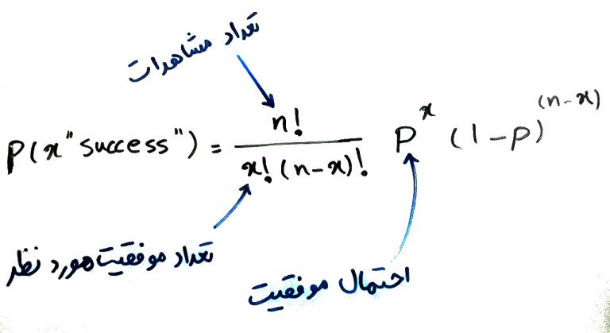
برای پاسخ به مسئلهی بالا، n = 10 است. x = 7 یعنی به دنبال تعدادِ دقیقاً ۷ مشاهده که success شوند، هستم و p = 0.8 است. با جایگذاریِ این اعداد در فرمول بالا، میتوانیم احتمال اینکه دقیقاً ۷ نفر از این ۱۰ بیمار که سکتهی مغزی کردهاند، زنده بمانند را به دست بیاوریم:
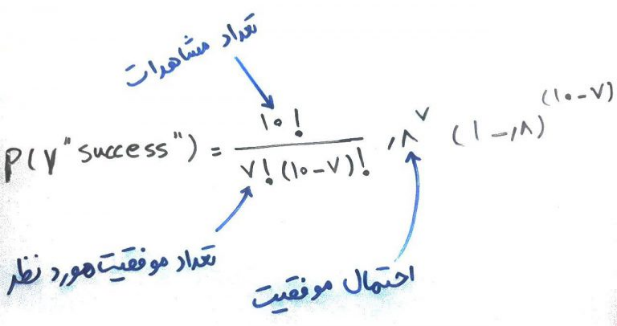
که نتیجه برابر ۰.۲۰ خواهد شد. یعنی به احتمال ۲۰ درصد، دقیقاً ۷ نفر زنده میمانند. البته اینکه دادههای ما از توزیع دو جملهای پیروی کنند، نیازمند چند شرط است. مثلاً اینکه هر کدام از پیشامدها مستقل از دیگری باشند. در مثال بالا، مثلاً اگر یک بیمار جدید که سکته کرده بود، رسید، زنده ماندن یا فوت کردنِ این بیمار ارتباطی با زنده ماندن یا فوت کردنِ بیمار قبلی نداشته باشد.
شرط دیگر هم این است که حتماً هر کدام از پیشامدها در دو حالت قرار بگیرند و حالت سومی وجود نداشته باشد. و شرط آخر هم اینکه احتمال موفقیت یا شکست در هر بار از پیشامدها برابر باشد. در مثال بالا، مثلاً احتمال زنده ماندنِ یک بیمار ۸۰ درصد و احتمال زنده ماندن بیماری دیگر ۹۰ درصد نباشد. همه یک احتمال برای زنده ماندن داشته باشند.
در مثالِ بالا، اگر بخواهیم ببینیم احتمالِ اینکه از بین این ۱۰ بیمار، ۰ یا ۱ بیمار زنده بمانند بایستی احتمال ۰ را حساب کرده، سپس احتمال ۱ را هم حساب کرده و آنها را با هم جمع کنیم.
همانطور که دیدید توزیع برنولی و دو جملهای از توزیعهای گسستهای هستند که کاربردهای فراوانی در بین دادهها و فرآیندهای مختلف و حل مسائل گوناگون دارند.
توزیع نرمال
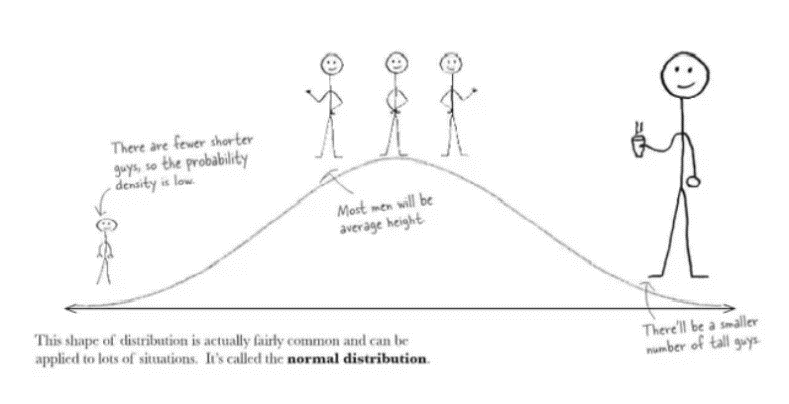
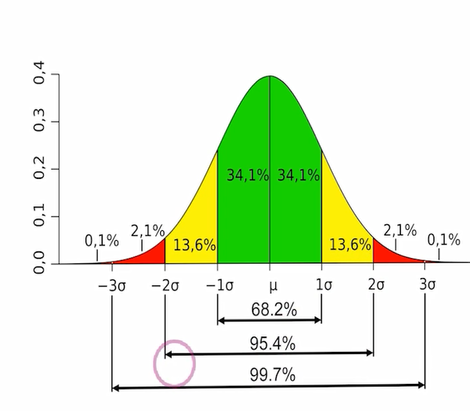
در نظریه آمار و احتمال، توزیع نرمال (Normal Distribution) یکی از مهمترین توزیعهای آماری است. البته به این توزیع گاهی «توزیع گاوسی» (Gaussian Distribution) یا توزیع «گاوس-لاپلاس» (Laplace-Gauss) گفته میشود. از آنجایی که این توزیع دارای منحنی به شکل زنگ است، گاهی به آن «منحنی زنگی شکل» (Bell Curve) نیز گفته میشود.
به عنوان مثال، قد افراد در یک جامعه توزیع نرمال است و یا میزان دمای هوا در طول یک سال توزیع نرمال است.
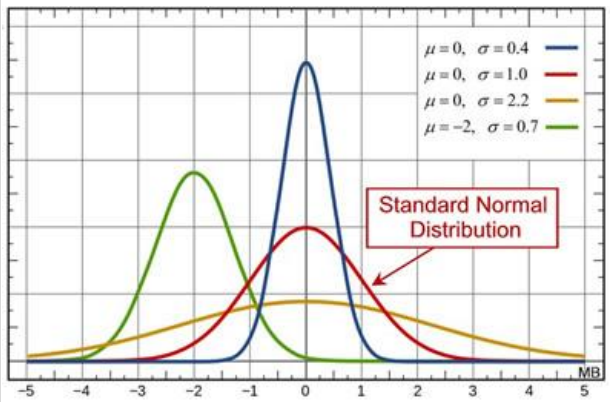
تابع چگالی
تابعِ چگالیِ احتمالِ یک متغیر تصادفی پیوسته به تابعی گفته میشود که انتگرال آن در هر بازه معین، برابر با احتمال قرار داشتن متغیر تصادفی در آن بازه است.
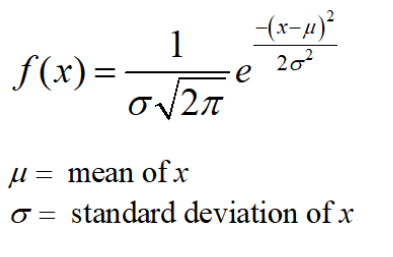
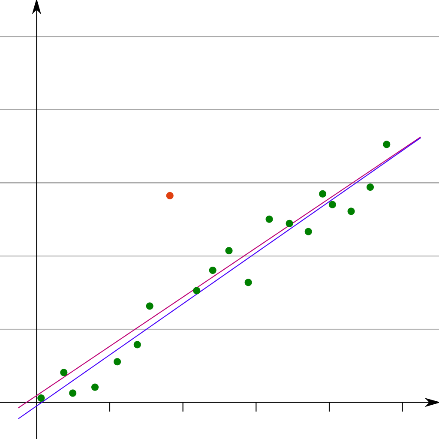
مشاهدات پرت
مشاهدات پرت مشاهداتی هستند که غلط نیستند اما از بدنه توزیع داده ها دور افتاده و پرت هستند.
محاسبه چندک و احتمال تجمعی
فرض کنید در توزیع نرمال قد افراد بخواهیم پیدا کنیم که مثلا پیدا کنیم که چند درصد از افراد ایرانی قد زیر 180 دارند یا به عبارت دیگر احتمال اینکه یک فرد ایرانی قدش زیر 180 باشد چقدر است؟ یعنی بازه ای که در محور x ها a کمتر از 180 باشد.
در این مثال باید پیدا کرد که مساحت فضای آبی رنگ چقدر است، بنابر این باید انتگرال F(x) را پیدا کنیم.
یا فرض کنیم که بخواهیم پیدا کنیم که چه قدی هست که 90% مرد های ایرانی کوچکتر از آن باشد؟ بنابر این باید چندک توزیع را نداریم ولی احتمال را داریم و به وسیله آن احتمال می شود آن قد را پیدا کرد.
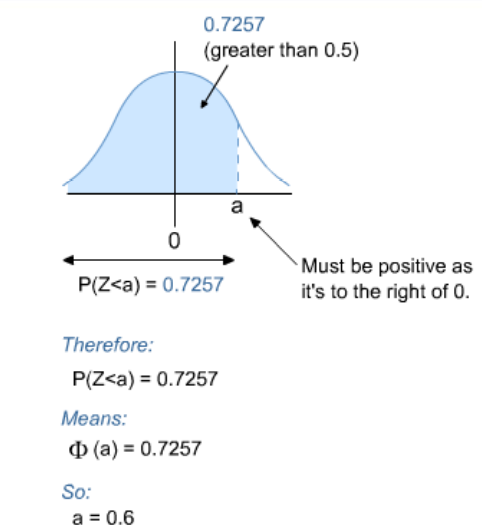
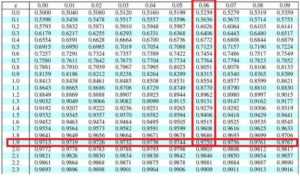
یکی از راه هایی که بخواهیم این سوالات را حل نماییم این است که از جداول توزیع نرمال که معمولا انتهای کتاب های آماری قرار دارد و نرم افزار ها نیز قابلیت محاسبه آن را دارند.
به عنوان مثال در تصویر زیر اگر بخواهیم، به دنبال چندکی از محور x هستیم که احتمال کمتر از آن برابر 0.975 باشد، کافی است که عدد 0.975 را در جدول پیدا کنیم و وصل کنیم به دو ستون و ردیف اصلی. بنابر این در این
سوال آن برابر است با 1.90 و 0.6 که می شود 1.96
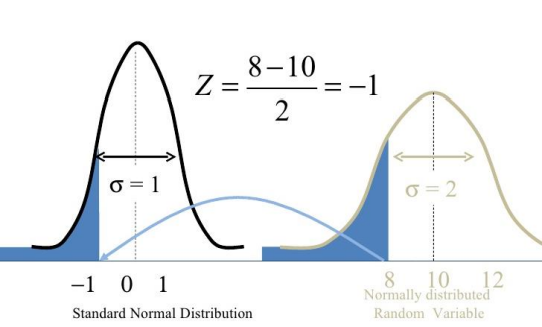
تبدیل توزیع
نکته: تبدیل های خطی توزیع را حفظ می کند؛ یعنی اگر یک توزیع در عبارت ax+b ضرب شود آن توزیع حفظ می شود.
برای تبدیل یک توزیع به توزیع نرمال از تابع Z استفاده می نماییم:
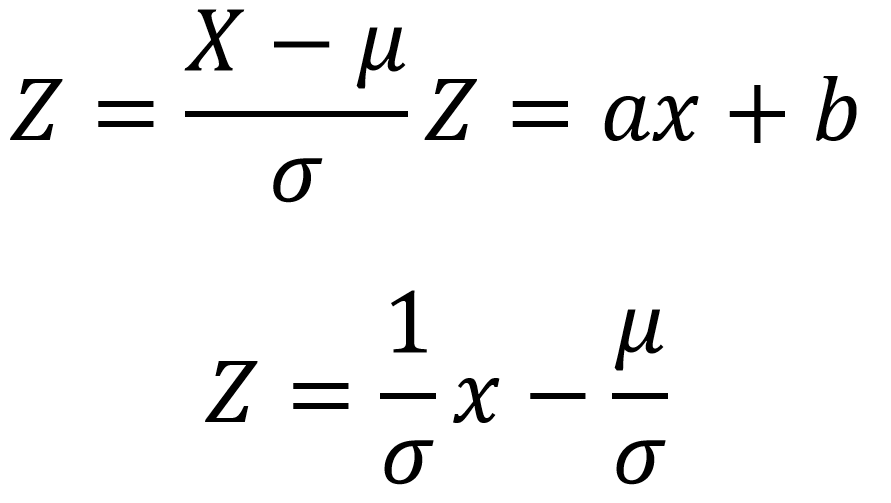
بنابراین استفاده از تابع Z توزیع را تغییر نمی دهد. Z هیچ وقت توزیعی که نرمال نیست را تبدیل به توزیع نرمال نمی کند و تبدیل Z فقط یک توزیع نرمال را تبدیل به توزیع نرمال استاندارد می کند.