الگوریتم K-نزدیک ترین همسایگی (k-Nearest Neighbors) یک روش ناپارامتری است که در دادهکاوی، یادگیری ماشین و تشخیص الگو مورد استفاده قرار میگیرد. بر اساس آمارهای ارائه شده در وبسایت kdnuggets الگوریتم k-نزدیکترین همسایگی یکی از ده الگوریتمی است که بیشترین استفاده را در پروژههای گوناگون یادگیری ماشین و دادهکاوی، هم در صنعت و هم در دانشگاه داشته است.
الگوریتم k-نزدیکترین همسایگی برای مسائل طبقهبندی و رگرسیون قابل استفاده است. اگرچه، در اغلب مواقع از آن برای مسائل طبقهبندی استفاده میشود. برای ارزیابی هر روشی به طور کلی به سه جنبه مهم آن توجه میشود:
1. در جدول ۱ الگوریتم نزدیکترین همسایگی با سهولت تفسیر خروجیها
2. زمان محاسبه
3. قدرت پیشبینی
الگوریتمهای «رگرسیون لجستیک»، «CART» و «جنگلهای تصادفی» (random forests) مقایسه شده است. همانگونه که از جدول مشخص است، الگوریتم k-نزدیکترین همسایگی بر اساس جنبههای بیان شده در بالا، نسبت به دیگر الگوریتمهای موجود در جایگاه مناسبی قرار دارد.
این الگوریتم اغلب به دلیل سهولت تفسیر نتایج و زمان محاسبه پایین مورد استفاده قرار میگیرد.

الگوریتم k-نزدیکترین همسایگی چگونه کار میکند؟
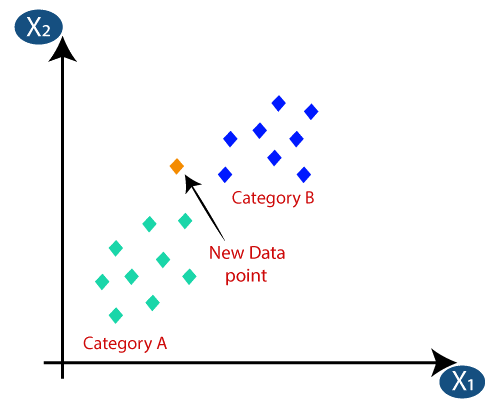
برای درک بهتر شیوه کار این الگوریتم، عملکرد آن با یک مثال ساده مورد بررسی قرار گرفته است. در شکل ۱ نحوه توزیع دایرههای قرمز (RC) و مربعهای سبز (GS) را مشاهده میکنید.
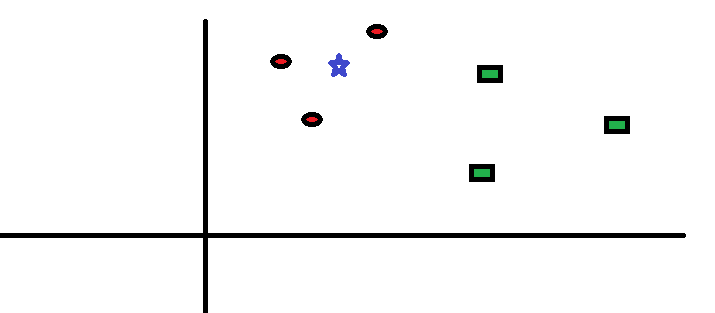
فرض کنید قصد پیدا کردن کلاسی که ستاره آبی (BS) متعلق به آن است را دارید (یعنی دایرههای قرمز). در این مثال در کل دو کلاس دایرههای قرمز و مربعهای سبز وجود دارند و ستاره آبی بر اساس منطق کلاسیک میتواند تنها متعلق به یکی از این دو کلاس باشد.
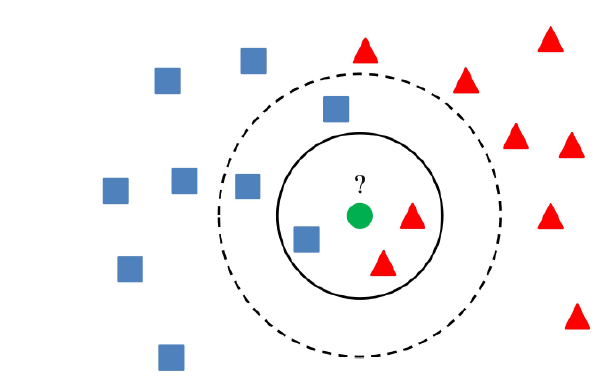
«K» در الگوریتم k-نزدیکترین همسایگی، تعداد نزدیکترین همسایههایی است که بر اساس آنها رأیگیری درباره وضعیت تعلق یک نمونه داده به کلاسهای موجود انجام میشود. فرض کنید k = ۳ است. یک دایره آبی دور سه تا از نزدیکترین همسایههای ستاره آبی ترسیم شده (شکل ۲) است. برای جزئیات بیشتر نمودار شکل ۲ را نگاه کنید.
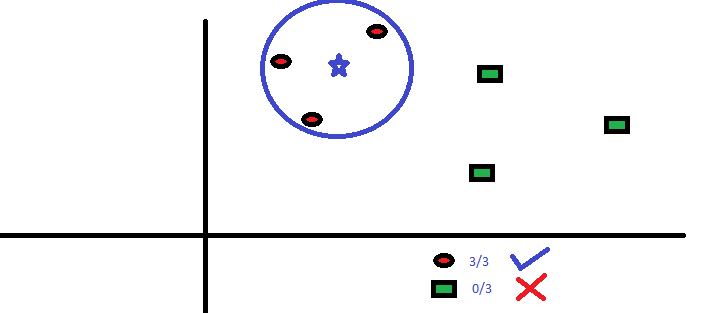
سه نقطه نزدیکتر به BS، همه دایرههای قرمز هستند. با میزان اطمینان خوبی میتوان گفت که ستاره آبی به کلاس دایرههای قرمز تعلق دارد. در این مثال، انتخاب بسیار آسان است چون هر سه نزدیکترین همسایه ستاره آبی، دایرههای قرمز هستند و در واقع هر سه رأی متعلق به دایرههای قرمز است. انتخاب پارامتر k در الگوریتم k-نزدیکترین همسایگی، بسیار حائز اهمیت است. در ادامه عوامل تاثیرگذار بر انتخاب بهترین k، مورد بررسی قرار میگیرند.
- پارامتر k چگونه انتخاب میشود؟
در ابتدا بهتر است تأثیر انتخاب k در الگوریتم k-نزدیکترین همسایگی بر نتایج خروجی مورد بررسی قرار بگیرد. اگر به مثال پیشین توجه کنید، میبینید که هر شش نمونه (دایرههای قرمز و مستطیلهای سبز) ثابت هستند و تنها انتخاب k میتواند مرزهای یک کلاس را دستخوش تغییر کند. در ادامه مرزهای دو کلاس که با انتخاب kهای گوناگون تغییر پیدا میکنند (شکل ۳) را مشاهده میکنید.

همانطور که از تصاویر مشهود است، با افزایش مقدار k، مرزهای کلاسها روانتر میشود. با افزایش k به سمت بینهایت، بسته به اکثریت مطلق نمونهها در نهایت یک کلاس آبی یا قرمز وجود خواهد داشت. نرخ خطاهای آموزش (training) و ارزیابی (evaluation) دو عاملی هستند که برای تعیین مقدار k مناسب به آنها نیاز داریم. نمودار خطی در شکل ۴ بر اساس مقدار خطای آموزش برای kهای گوناگون ترسیم شده است.

چنانکه مشاهده میکنید، نرخ خطا هنگامیکه k = ۱ است، برای نمونههای آموزش صفر باقی میماند. این امر بدین دلیل است که نزدیکترین نقطه به هر داده آموزش، خود آن داده است. بنابراین نتایج پیشبینی با k = ۱ صحیح است. اگر k = ۱ باشد نمودار خطای ارزیابی نیز روند مشابهی دارد. نمودار خطای ارزیابی با مقادیر گوناگون k در شکل ۵ نمایش داده شده است.

هنگامی که k = ۱ است مرزها دچار بیش برازش (overfit) شدهاند. بنابراین نرخ خطا کاهش پیدا کرده و در واقع به حداقل میزان خود میرسد و با افزایش k مقدار خطا نیز افزایش پیدا میکند. برای انتخاب مقدار بهینه k میتوان دادههای آموزش و ارزیابی را از مجموعه داده اولیه جدا کرد. سپس با رسم نمودار مربوط به خطای ارزیابی مقدار بهینه K را انتخاب کرد.
این مقدار از k باید برای همه پیشبینیها مورد استفاده قرار بگیرد و در واقع برای همه مراحل پیشبینی باید از یک k مشخص استفاده شود.
الگوریتم KNN یکی از انواع الگوریتم های جعبه سیاه با مدل یادگیری با نظارت می باشد که قابلیت بکارگیری در انواع مسائل رده بندی و رگرسیون را دارد.
ایده اصلی الگوریتم KNN اینست که چیزهای مشابه در نزدیکی هم قرار دارند. به عبارتی با اندازه گیری میزان فاصله بین رکوردها، می توان این فرض را در نظر گرفت که رکوردهای نزدیکتر به هم دارای مشابهت هستند.
کبوتر با کبوتر باز با باز، کند همجنس با همجنس پرواز

معیارهای متفاوتی برای اندازه شباهت می توان در نظر گرفت:
توابع فاصله
توابع زیادی برای اندازهگیری فاصله بین اشیاء، با ویژگیهای کمی وجود دارد. «توابع فاصله» (Distance Functions) در تکنیکهای دادهکاوی بخصوص در خوشهبندی، کاربردهای زیادی دارند.
در این متن ابتدا به معرفی خصوصیات تابع فاصله میپردازیم و سپس شیوه محاسبه فاصله را براساس چند روش از جمله «فاصله اقلیدسی» (Euclidean Distance)، «فاصله منهتن» (Manhattan Distance) و «فاصله مینکوفسکی» (Minkowski Distance) بررسی میکنیم. این توابع فاصله بیشتر برای اندازهگیری میزان عدم شباهت در مباحث دادهکاوی به کار میروند.
● فاصله اقلیدسی
با استفاده از «فاصله اقلیدسی» (Euclidean Distance) کوتاهترین فاصله بین دو نقطه بر طبق رابطه فیثاغورث، محاسبه میشود. اگر x و y دو نقطه با p مولفه باشند، فاصله اقلیدسی بین این دو به صورت زیر قابل محاسبه است:
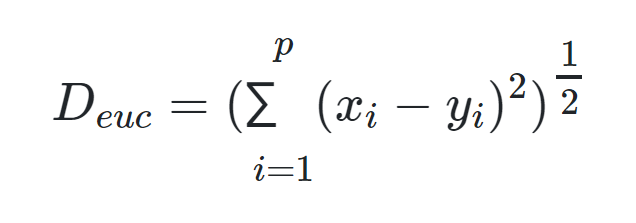
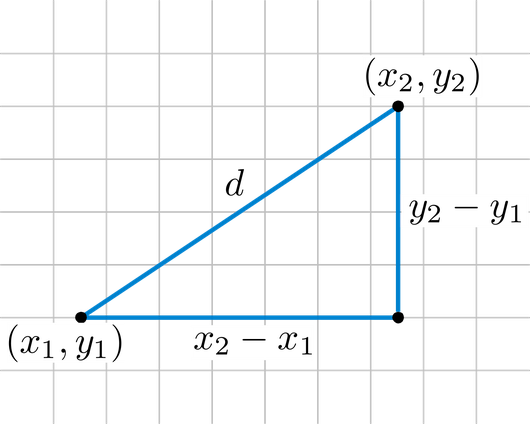
در تصویر زیر، فاصله اقلیدسی بین دو نقطه با مختصات (x1,y1)(x1,y1) با (x2,y2)(x2,y2) نشان داده شده است.
در ادامه به بررسی خصوصیات تابع فاصله برای فاصله اقلیدسی میپردازیم.
- فاصله اقلیدسی باید نامنفی باشد: مشخص است که این رابطه مقداری نامنفی دارد زیرا از مجموع مربعات تفاضلها ساخته شده است.
- وجود رابطه انعکاسی برای فاصله اقلیدسی: برای نقطههای x و y با مقدار مولفههای یکسان، فاصله اقلیدسی برابر با صفر خواهد بود. همچنین زمانی که فاصله اقلیدسی صفر باشد باید همه مربعات تفاضلها صفر باشند، در نتیجه دو نقطه بر هم منطبق هستند.
- رابطه مثلثی برای فاصله اقلیدسی: اگر دو نقطه A به مختصات (x1,y1) و نقطه B به مختصات (x2,y2) وجود داشته باشند و همچنین (x1−x2)=x;(y1−y2)=y در نظر گرفته شود، میتوان نوشت:
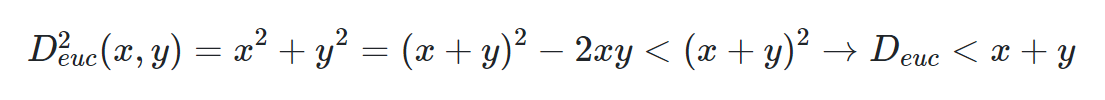
که نشان میدهد فاصله اقلیدسی در نامساوی مثلثی صدق میکند. بر طبق تصویر زیر، نیز میتوان مشاهده کرد که فاصله اقلیدسی در رابطه مثلثی صادق است.
فرض کنید دو نقطه A و B در فضای دو بعدی با مختصات (2,4) و (4,5) وجود داشته باشد. فاصله این دو نقطه بر حسب فاصله اقلیدسی برابر است با:
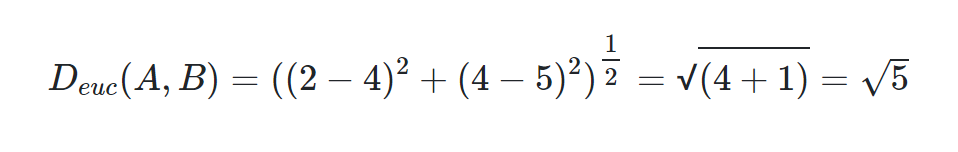
رایج ترین معیار فاصله که در صورت کم بودن تعداد ویژگی ها به علت سادگی و شهودی بودن آن، نتایج بسیار خوبی خواهد داشت.
● فاصله منهتن
- درک شهودی و تجسم این معیار نسبت به فاصله اقلیدسی سخت تر است ولی معمولا در داده های با ابعاد بالا عملکرد خوبی نشان می دهد.
- اگر به جای مربع فاصله بین مولفهها، از قدر مطلق فاصله بین مولفههای نقاط استفاده شود، تابع فاصله را «منهتن» (Manhatan) مینامند. این نام به علت تقاطع منظم خیابانها در محله منهتن نیویورک انتخاب شده است. البته این فاصله گاهی به نام «فاصله تاکسی» (Taxicab) یا «بلوک شهری» (City Block) نیز نامیده میشود.
- اگر x و y دو نقطه با p مولفه (P بعدی) باشند، شیوه محاسبه فاصله منهتن به صورت زیر خواهد بود:
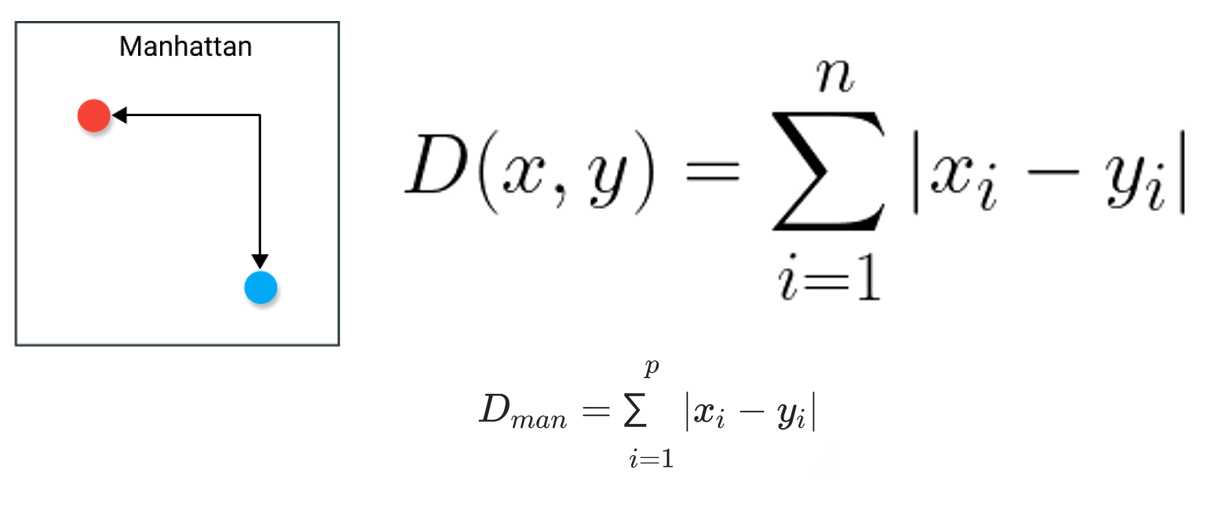
همانطور که در تصویر زیر دیده میشود، اگر محور افقی و عمودی به طولهای برابر و مساوی با ۱ تقسیم شده باشند، بین دو نقطه سیاه رنگ، مسیرهای مختلفی با فاصله منهتن یکسان وجود دارد. خطهای قرمز و آبی و زرد، مسیرهایی با فاصله منهتن ۱۲ بین این دو نقطه هستند، در حالی که خط سبز نشان دهنده فاصله اقلیدسی است که با طول برابر با کوتاهترین مسیر را (در صورت وجود) نشان میدهد.
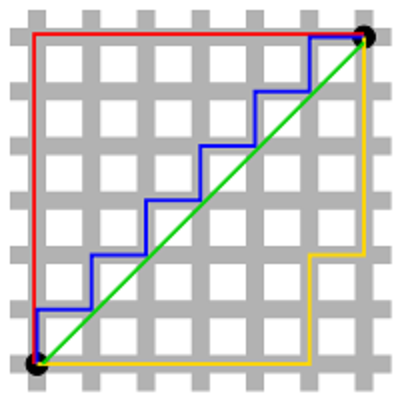
براساس نقاط مربوط به مثال قبلی، فاصله منهتن بین دو نقطه A و B به صورت زیر محاسبه میشود:

نحوه عملکرد الگوریتم KNN:
- تعیین مقدار K
- محاسبه مقدار فاصله (معیار شباهت) برای رکورد مورد نظر با تمامی رکوردهای موجود
- مرتب سازی شماره (اندیس) رکوردها بر اساس کوچکترین مقادیر فاصله
- انتخاب K رکورد اول از لیست مرتب سازی شده
- پیش بینی مقدار هدف
- مسئله رده بندی: محاسبه مد (بیشترین فراوانی) کلاس هدف در K رکورد منتخب
- مسئله رگرسیون: محاسبه میانگین (میانه) مقدار هدف در K رکورد منتخب
در مسائل رده بندی، معمولا از مقادیر فرد برای K استفاده می شود تا در رای گیری کلاس هدف، اطمینان از انتخاب کلاس داشته باشیم.
تنها چالش مهم این الگوریتم تعیین مقدار K می باشد:
در صورتی که مقدار K کوچک انتخاب شود، منجر به نتایج ناپایدار می شود و با انتخاب مقادیر بزرگ K می توان ناحیه تصمیم گیری را هموارتر نمود و نتایج پایدارتری را ایجاد نمود؛ ولی در مسائل رده بندی نامتوازن ریسک نادیده گرفتن کلاس مینور (کلاس حداقلی) را افزایش داده و دچار خطای جدی در پیش بینی درست خواهد شد.
- انتخاب K بهینه
معمولا با انتخاب طرح اعتبارسنجی متقابل و برای مقادیر مختلف K، مدل KNN اجرا شده و مقدار میانگین خطای پیش بینی به ازای هر K محاسبه و در نمودار نمایش داده می شود. مقدار K با کمترین میزان خطا، به عنوان K بهینه انتخاب می گردد.
یکی از کاربردهای مهم الگوریتم KNN، صرفا یافتن نزدیکترین موارد مشابه می باشد. بنابراین در این کاربرد، حضور فیلد هدف الزامی نیست و گزارش لیستی از K رکورد مشابه هدف مسئله می باشد.
مثال 1: فرض کنید تعداد 100 پرونده اظهارنامه مالیاتی متخلف (دارای عددسازی و مقادیر غیر واقعی) را شناسایی کرده ایم. با استفاده از این الگوریتم می توان به ازای هر یک از این پرونده ها، تعداد K پرونده مشابه از میان هزاران پرونده در صف ممیزی را استخراج نمود و با الویت بازرسی بالاتر، در زمانی سریعتر به سایر پرونده های متخلف دسترسی پیدا کنیم.
مثال 2: فرض کنید به عنوان یک اپلیکیشن پخش موزیک، مجموعه داده هایی متشکل از ژانر، ابزار موسیقی، نوازنده، خواننده و امتیاز کاربران را برای هر یک از ترانه های آرشیو خود در دسترس دارید. با استفاده از الگوریتم KNN می توان برای هر ترانه به تعداد K ترانه با نزدیکترین میزان شباهت را تعیین نمود و به عنوان یک سیستم پیشنهاد دهنده (Recommender Systems) به کاربران اپلیکیشن، ترانه پیشنهادی بعدی را معرفی کرد.
الگوریتم KNN از مجموعه مدلهای استنتاج مبتنی بر موارد (Case Based Reasoning) می باشد و بر خلاف سایر الگوریتم های دیگر هیچ مدلی بر روی داده ها برازش داده نمی شود. در نتیجه:
-
- به منظور اجرای الگوریتم برای هر رکورد، نیاز به حضور تمامی داده های موجود در حافظه (Memory) می باشد.
- اجرای الگوریتم در داده های با ابعاد بالا (رکوردها و ویژگی ها زیاد) بسیار کند خواهد شد. به همین دلیل جزو دسته مدلهای تنبل (Lazy) قرار می گیرد.
